Системы со сложной структурой

Системы, для которых качественный (структурный) анализ расчётной схемы не может быть полностью выполнен с использованием только типовых способов (приёмов) геометрически неизменяемого соединения дисков, называются с и с т е м а м и с о с л о ж н о й с т р у к т у р о й.

К таким системам относится сооружение, изображённое на рис. 1.44.

Для выполнения качественного анализа систем со сложной структурой могут применяться:

1) непосредственное исследование кинематической природы связей (описание дано выше);

2) способ замены связей;

3) аналитический признак геометрической неизменяемости системы.

При реализации первого подхода, как правило, не требуется анализировать все связи системы – достаточно оценить некоторые из них (а при W = 0 – возможно, даже одну). Например, в системе, представленной на рис. 1.44, в силу того, что W = 0, все связи должны быть необходимыми – лишь в этом случае структура её будет правильной. Проверим кинематическое качество какой-либо связи, в частности, вертикальной линейной связи ЕК. Если это необходимая связь, то для неё должно быть выполнено условие 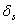0 (см. табл. 2).

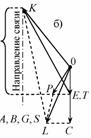
Рис.1.45

В соответствии с общей схемой выявления кинематической природы связи удаляем её и полученной системе, превратившейся в механизм с одной степенью свободы, задаём возможные перемещения, показанные схематически штриховыми линиями на рис. 1.45, а (при этом используется гипотеза отвердения). Искомая величина 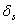есть проекция на направление удалённой линейной связи ЕК взаимного (относительного) перемещения соединяемых ею точек Е и К. Задав отличное от нуля (числовое значение не играет никакой роли) малое перемещение какой-либо точки (например, С), определяем перемещения всех остальных характерных точек механизма (узлов, где соединяются диски). Для этого можно использовать:

а) мгновенные взаимные центры вращения дисков;

б) план мгновенных перемещений точек механизма (подобен плану мгновенных скоростей).

На рис. 1.45, б представлен план перемещений, на котором векторы 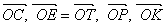и линии LС, PL, KL и РТ ортогональны одноимённым линиям на схеме механизма (рис. 1.45, а). Отрезок ЕК на плане – полное взаимное перемещение точек Е и К; его проекция на направление удалённой связи (в рассматриваемом случае – на вертикаль) и есть перемещение 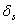. Оно получилось отличным от нуля – признак того, что исследованная связь – необходимая. Её возвращение в систему устраняет возможность возникновения любых перемещений при отсутствии деформаций элементов (план перемещений вырождается в точку), следовательно, система – геометрически неизменяемая, а поскольку W = 0, то и статически определимая.

В двух других вышеуказанных вариантах качественного анализа систем со сложной структурой, основанных на способе замены связей и аналитическом признаке геометрической неизменяемости, используются, в отличие от остальных подходов, статические характеристики связей.

Сущность способа замены связей состоит в следующем. Если структура системы правильная, то любое конечное воздействие вызывает в ней, в случае устойчивого равновесия, единственное напряжённо-деформированное состояние с конечными значениями перемещений и силовых факторов, в том числе реакцию S некоторой связи, кинематическую природу которой требуется определить. Для системы со сложной структурой может оказаться трудоёмкой процедура составления и решения уравнений, с помощью которых находится S. Для упрощения осуществляется замена связей: исследуемая связь удаляется с приложением вместо неё реакции S, и в систему вводится новая (заменяющая) связь, причём таким образом, чтобы получилась система с простой структурой. Реакция заменяющей связи , согласно принципу суперпозиции, может быть представлена как сумма её составляющих – 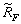(от некоторого воздействия – нагрузки) и 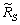(от реакции S удалённой исследуемой связи):

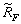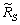=+. (7)

Величина 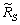может быть записана в ви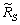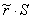де =, где 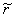– реакция заменяющей связи от усилия S = 1. Поскольку силовой фактор S обеспечивает равновесие системы с удалённой связью при действии нагрузки, то заменяющая связь в работу не включается, и усилие в ней равно нулю: = 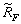+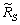= 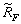+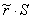= 0, откуда S = –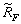/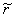. Очевидно, что для получения конечного значения усилия S нужно, чтобы знаменатель дроби не был нулевым, следовательно,

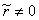– (8)

признак необходимой связи по способу замены связей.

Если для получения системы с простой структурой требуется произвести замену не одной, а нескольких (n) связей, то признак группы необходимых связей принимает вид

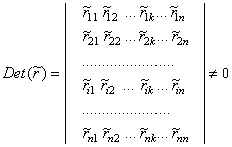, (9)

где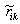– реакция i -й заменяющей связи от единичного усилия в удалённой k -й связи (от S_k = 1).

Для систем с W = 0 требования (8) и (9) являются необходимыми и достаточными условиями геометрической неизменяемости.

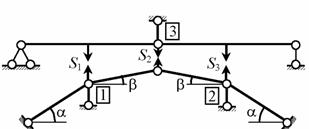
Рис.1.46

Например, в рассматриваемой системе со сложной структурой (см. рис. 1.44) удаляем одновременно три линейные связи, прикладывая вместо них реакции S ₁ , S ₂ и S ₃ (рис. 1.46), а затем вводим в систему три заменяющие связи, обозначенные цифрами 1, 2 и 3 в прямоугольниках. Последовательно задавая S ₁ = 1, S ₂ = 1 и S ₃ = 1, определяем вызываемые ими реакции заменяющих связей и формируем матрицу :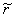

,

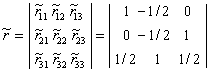компоненты второго столбца которой вычислены при 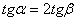. Определитель этой матрицы Det (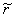) = –3/2 – это означает, что три исследованные связи – необходимые, что является гарантией геометрической неизменяемости системы. Заметим, что для неё было бы достаточно осуществить замену лишь одной связи. Читателю предлагается самостоятельно убе-диться в том, что при 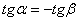(неудачная – зигзагообразная геометрия нижней части системы) получается Det (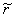) = 0 – признак мгновенной изменяемости системы.

И наконец, рассмотрим аналитический признак геометрической неизменяемости. Он формулирует условие невырожденности системы разрешающих уравнений, формируемых для вычисления параметров напряжённо-деформированного состояния сооружения. Для линейно деформируемой системы (физические свойства материала которой описываются законом Гука, перемещения малы и расчётная схема не изменяется в процессе деформирования) разрешающие уравнения могут быть представлены в виде линейных алгебраических уравнений 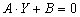, где Y – вектор неизвестных силовых факторов и/или перемещений, А – матрица коэффициентов, зависящая от собственных (геометрических, жесткостных и др.) свойств сооружения, В – вектор параметров, отражающих влияние заданных воздействий. Единственное решение СЛАУ возможно лишь в случае, когда Det (A)– это и есть необходимое и достаточное аналитическое условие геометрической неизменяемости системы.

Заключение

Кинематический анализ должен предшествовать расчёту всегда, когда это практически возможно, – во всяком случае, для систем со сравнительно небольшим числом элементов. К сожалению, многоэлементные, особенно пространственные, системы могут иметь достаточно сложную структуру, трудно поддающуюся исследованию с помощью рассмотренных выше приёмов, требующих использования геометрических представлений, которые, ко всему прочему, плохо реализуются в компьютерных программах. В этих случаях может оказаться полезным использование аналогий с известными решениями, накопленный опыт и т.п. Если же кинематический анализ сложной системы оказывается неоправданно трудоемким, то он может не выполняться – при этом попытка автоматизированного компьютерного расчёта системы с не выявленной заблаговременно геометрической или мгновенной изменяемостью приведет к тому, что в процессе машинного счета будет обнаружена невозможность решения вырожденной системы уравнений или будут получены несоразмерно большие значения усилий (признак систем, близких к мгновенно изменяемым).

По мере накопления опыта кинематический анализ может выполняться не обязательно по вышеизложенной полной (двухэтапной) схеме, так как для систем с простой структурой во многих практических случаях оказывается достаточно только структурного анализа, чтобы сделать заключение о кинематической природе системы.

Теперь, когда понятны основное предназначение кинематического анализа (обеспечение функции «входного контроля» расчётной схемы системы) и методика его выполнения, отметим его прикладное значение:

– во-первых, выявленная в ходе структурного анализа последовательность образования системы (порядок соединения и добавления элементов и частей) позволяет для статически определимых систем определить рациональный порядок расчёта по следующему правилу: расчёт СОС выполняется в порядке, обратном последовательности её образования. Это значит, что определение реакций начинается со связей, наложенных на диски в последнюю очередь в процессе синтеза системы, и заканчивается реакциями связей, введённых на первом шаге образования системы. Иными словами, чем раньше появилась связь в ходе создания системы из начального набора несвязанных элементов-дисков, тем позднее в процессе расчёта определяется её реакция;

– во-вторых, с инженерной, практической точки зрения структурный анализ расчётной схемы сооружения является основой для назначения правильной последовательности укрупнительной сборки из отдельных конструктивных элементов и монтажа в проектном положении реальных строительных конструкций, в результате чего может быть обеспечена неизменяемость возводимого сооружения на каждом технологическом шаге.

Дата добавления: 2014-01-11