Примеры кинематического анализа

Пример 1.1. Произвести кинематический анализ системы (рис.1.14).

Определяем степень свободы системы по формуле П.Л.Чебышева:

W = 3Д – 2Ш – С₀,

где Д – число дисков, Ш – число простых шарниров, С₀ – количество стержней.

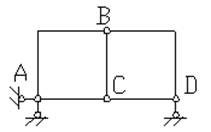
Рис.1.14

Отбрасывая все шарниры и опорные стержни, находим, что система состоит из пяти дисков (Д =5). Отбрасывая опорные стержни, определяем число шарниров, приведенных к простым (Ш =6: по два в точках В и С, по одному – в точках А и Д). Число опорных стержней - С₀ =3.

Отсюда W = 3∙5 – 2∙6 – 3 = 0, то есть система может быть геометрически неизменяемой и статически неопределимой. Чтобы убедиться, что это так, выполним анализ структуры системы. Так как диски АВ, ВС и АС связаны тремя шарнирами А, В и С, не лежащими на одной прямой, то они образуют диск, к которому жестко присоединен диск ВД с помощью шарнира В и стержня СД, ось которого не проходит через центр шарнира. Эта неизменяемая фигура жестко присоединена к земле с помощью трех стержней, не пересекающихся в одной точке. Таким образом, система (рис.1.14) геометрически неизменяема и не является мгновенно изменяемой.

Пример 1.2. Выполнить кинематический анализ системы (рис.1.15).

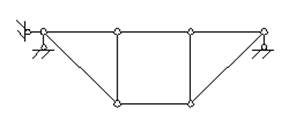
Рис.1.15

Так как система является шарнирно-стержневой, то для определения ее степени свободы используем формулу (1.2):

W = 2У – С – С₀,

где У – число узлов фермы; С – число внутренних стержней; С₀ – число опорных стержней.

Здесь У = 6, С = 8, С₀ = 3, следовательно, W = 2∙6 – 8 – 3 = 1.

Таким образом, система имеет одну степень свободы, и не может использоваться как строительная конструкция.

Пример 1.3. Исследовать ферму (рис.1.16).

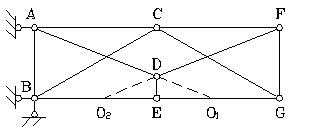
Рис.1.16

По формуле (1.2) определяем степень свободы фермы: W = 2∙7 – 11 – 3 = 0, следовательно, система может быть геометрически изменяемой и статически определимой.

Проанализируем систему. Она состоит из трех дисков – треугольники АВС, CFG и стержень DЕ, связанных между собой стержнями ВЕ, АD, ЕG, DF, которые можно заменить фиктивными шарнирами О₁, О₂ и шарниром С. Следовательно, можно сделать вывод: все стержни соединены между собой жестко и прикрепляются к земле так же жестко с помощью трех стержней, не пересекающихся в одной точке.

Для проверки системы на мгновенную изменяемость применим способ нулевой нагрузки – определим опорные реакции и усилия во всех стержнях при условии, что внешней нагрузки нет. Из условий равновесия всей системы (Σ М_А = 0; Σ М_В = 0; Σ У =0) находим, что опорные реакции равны нулю. Вырезая узел Е и проектируя все силы на вертикаль, находим, что усилие в вертикальном стержне N_DЕ = 0. Затем, записывая уравнения проекций двух сил, сходящихся в узле D (третья сила - N_DЕ = 0), на направления нормалей к этим стержням, находим, что усилия в стержнях DА и DF также равны нулю. Наконец, рассматривая равновесие узлов A, F, B, G, находим, что усилия во всех стержнях системы при отсутствии нагрузки равны нулю, следовательно, система неизменяемая.

Пример 1.4. Выполнить кинематический анализ системы (рис.1.17,а).

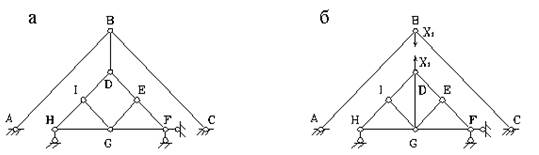
Рис.1.17

По формуле (1.2) определяем степень свободы: W = 2∙9 – 11 – 7 = 0, то есть система обладает необходимым минимумом связей, чтобы быть геометрически неизменяемой. Для проверки того, является ли система действительно неизменяемой, используем метод замены стержней. Выберем заменяющую систему (рис.1.17,б). Здесь отброшен стержень ВD, а его действие заменено силами Х₁, и добавлен заменяющий стержень DG. Выбранная заменяющая система неизменяема: стержни АВ, ВС и земля жестко соединены тремя шарнирами, не лежащими на одной прямой. А нижняя часть системы неизменяема, поскольку состоит из треугольника (например, GHI), к которому жестко прикреплены все остальные узлы с помощью диад, и все это прикреплено к земле тремя опорными стержнями.

Теперь определим усилие в заменяющем стержне от сил Х₁ = 1. Вырезая последовательно узлы E, I, G и рассматривая их равновесие, получим, что усилие в заменяющем стержне равно нулю, следовательно, исходная система - мгновенно изменяемая.

Пример 1.5. Произвести анализ образования системы, показанной на рис.1.18.

Рис.1.18

Вначале определяем степень свободы системы. Поскольку система является шарнирно-стержневой - воспользуемся формулой W = 2У – С – С₀. Число узлов системы У =6, число стержней системы С =8, число опорных стержней С ₀=3, следовательно, W = 2∙6 – 8 – 3 = 12 - 1 = +1. Система имеет одну степень свободы и не может быть использована в качестве строительной конструкции.

Пример 1.6. Произвести анализ образования системы, показанной на рис.1.19, а.

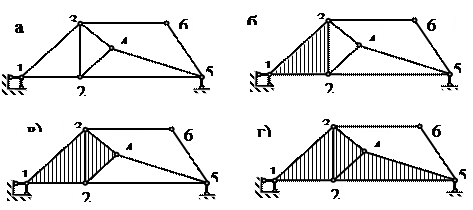
Рис.1.19

1. Пользуясь формулой W = 2У – С – С₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =6, число стержней системы С =9, число опорных стержней С ₀=3, следовательно, W = 2∙6 – 9 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть неизменяемой и статически определимой.

2. Проводим анализ структуры системы. Рассмотрим треугольник 123, который в соответствии с третьим признаком является неизменяемой системой. Считая его жестким диском (заштрихован на рис. 1.19, б), присоединим к нему двумя стержнями (3-4 и 2-4) узел 4. Эти стержни не лежат на одной прямой, следовательно, на основании первого принципа узел 4 неподвижно прикреплен к диску 123. Полученная система также является жестким диском (заштрихован на рис.1.19, в). Прикрепив к нему двумя стержнями (4-5 и 2-5) узел 5 снова получим жесткий диск, заштрихованный на рис.1.19, г). К этому диску присоединим двумя стержнями (3-6 и 5-6) не лежащими на одной прямой последний узел 6.

Поскольку система образована в соответствии с принципами образования структурно неизменяемых систем, она неизменяема и не является мгновенно изменяемой. К земле система прикреплена так же жестко, с помощью трех опорных стержней, не пересекающихся в одной точке.

Пример 1.7. Произвести кинематический анализ системы, показанной на рис. 1.20.

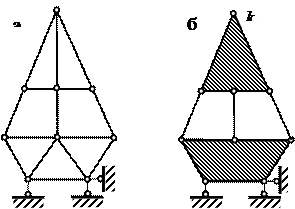
Рис.1.20

1. Пользуясь формулой W = 2У – С – С₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =9, число стержней системы С =15, число опорных стержней С ₀=3, следовательно, W = 2∙9 – 15 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть геометрически неизменяемой.

2. Проводим анализ структуры системы. Вначале найдем заведомо неизменяемые части системы – два диска, образованные треугольниками (заштрихованы на рис. 1.21, б). Они соединены тремя стержнями. Однако эти стержни пересекаются в одной точке (т. k на рис. 1.21, б). Следовательно, система мгновенно изменяемая.

Пример 1.8. Проанализировать систему, изображенную на рис. 1.21.

Система состоит из четырех дисков (AС, СE, EF и FH) т.е. Д= 4. Число шарниров Ш= 3 (все шарниры простые). Число опорных стержней С ₀=2+1∙4=6. Степень свободы системы по формуле W = 3Д – 2Ш – С₀ = 3∙4-2∙3-6=0.

Рис.1.21

Необходимое условие неизменяемости системы удовлетворено. Производим анализ структуры. Диск АС присоединен к земле тремя опорными стержнями, не пересекающимися в одной точке. Такое прикрепление обеспечивает неподвижность диска АС. К нему шарниром С и к земле опорным стержнем в точке D прикреплен диск СЕ. При этом ось стержня D не проходит через шарнир С. К полученной неизменяемой системе стержнем EF и двумя опорными стержнями в точках G и H присоединен диск FH. Эти три стержня не пересекаются в одной точке.

Таким образом, рассматриваемая система неизменяема и не является мгновенно изменяемой.

Пример 1.9. Проверить геометрическую неизменяемость системы, приведенной на рис. 1.22.

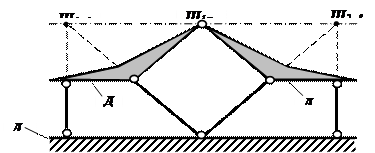
Рис.1.22

Здесь: Д =2; Ш =1; С _о =4. По формуле W = 3Д – 2Ш – С₀ = 3∙2-2∙1-4=0.

Следовательно, система имеет необходимое количество связей, чтобы неизменяемой. Проанализируем ее структуру.

Вместе с землей система состоит из трех дисков, соединенных между собой шарниром Ш_{1 – 2} и четырьмя стержнями, эквивалентными условным шарнирам Ш_{1 – 3} и Ш_{2– 3}.

Так как три шарнира, соединяющие три диска, лежат на одной прямой, система мгновенно изменяема.

Дата добавления: 2014-01-11