Представление данных в ЭВМ

Источниками и носителями информации могут быть сигналы любой природы: текст, речь, музыка и т.д. Однако хранение и перера­ботка инфор­мации в ее естест­венном виде неудобна, а иногда и невозможна. В таких слу­чаях применяется коди­рование. Ко­дом называется правило, по ко­торому со­поставляются различные алфавиты и слова (они появились в глу­бокой древно­сти в виде тайнописи, когда ими пользо­вались для засекречивания важ­ного со­общения). Исторически пер­вый уни­версальный код, предназначенный для передачи со­обще­ний, связан с именем изобре­тателя телеграфного аппарата Морзе и известен как аз­бука Морзе, где каждой букве или цифре соответст­вует своя последовательность из крат­ковременных, называемых точками, и длительных - тире сигналов, разделяе­мых пау­зами.

Компьютер, как из­вестно, может обрабатывать информацию, представ­ленную в чи­словой форме. Существуют различные способы записи чисел. Совокупность прие­мов записи и наименования чисел называется сис­темой счисления. Можно ука­зать два основных класса, на которые разделя­ются системы счис­ления - пози­ционные и непо­зиционные. Примером по­зи­цион­ной системы счисле­ния явля­ется десятичная, непозиционной - римская сис­тема счисления.

В непозиционных системах количественное значение разряда определя­ется только его изображением и не зависит от его места (позиции) в числе. В ней вводится ряд символов для представления основных чисел, а остальные числа - результат их сложения и вычитания. Основные символы для обозна­чения десятичных разрядов в римской системе счисления: I – один, X – де­сять, C – сто, M – тысяча и их половины V – пять, L – пятьдесят, D – пять­сот. Натуральные числа записываются при помощи повторения этих цифр (например, II – два, III – три, XXX – тридцать, CC – двести). Если же боль­шая цифра стоит перед меньшей цифрой, то они складываются, если на­обо­рот – вычитаются (например, VII – семь, IX – девять). В непозиционных системах счисления не представля­ются дробные и отрица­тель­ные числа, по­этому нас будут интересовать только по­зицион­ные системы счисле­ния.

Система счисления называется позиционной, если значение числа в ней оп­ределяется как символами, принятыми в системе, так и положением (пози­цией) этих символов в числе. Напри­мер:

123,45 = 1∙10 ² + 2∙10 ¹ + 3∙10 ⁰ + 4∙10 ^–1 + 5∙10 ^–2,

или, в общем виде:

X _(q) = x _n-1 q ^n-1 + x _n-2 q ^n-2 + … + x ₁ q ¹ + x ₀ q ⁰ + x _-1 q ^-1 + x _-2 q ^-2 + … + x _-m q ^–m .

Здесь X _(q) – запись числа в системе счисления с основанием q;

x _I – натуральные числа меньше q, т.е. цифры;

n – число разрядов целой части;

m – число разрядов дробной части.

Записывая слева направо цифры число, мы получим закодированную за­пись числа в q -ичной системе счисления.

X _(q) = x _n-1 x _n-2 x

₁ x ₀, x _-1 x _-2 x _-m.

В информатике, вследствие применения электронных средств вычисли­тельной техники, большое значение имеет двоичная система счисления, q = 2. На ранних этапах развития вычислительной техники арифметические операции с действительными числами производились в двоичной системе ввиду про­стоты их реализации в электронных схемах вычислительных машин. Отметим, что принци­п действия базовых элементов цифровых вычислительных машин осно­ван на двух устойчивых со­стояниях - проводится или нет электрический ток, или в каком направлении намагничен магнитный носитель и т.д. и для записи двоичного числа достаточно использовать только две цифры 0 и 1, соответствующих каждому из состояний. Таблица сложения и таб­лица ум­но­жения в двоичной системе будет иметь по четыре пра­вила. И для реализации поразрядной арифметики в компьютере потребуется вместо двух таблиц по сто правил в десятичной системе счисления две таб­лицы по четыре правила в двоичной.

0 + 0 = 0	0 * 0 = 0
0 + 1 = 1	0 * 1 = 0
1 + 0 = 1	1 * 0 = 0
1 + 1 = 10	1 * 1 = 1

Соответственно на аппаратном уровне вместо двухсот электронных схем – восемь. Однако запись числа в двоичной системе счисления значи­тельно длиннее записи того же числа в десятичной системе счисления. Это гро­моздко и неудобно для использования, так как обычно человек может од­но­временно воспринять не более пяти-семи еди­ниц информации. Поэтому, на­ряду с двоичной системой счисления, в инфор­матике имеют хождение вось­меричная (в ней запись числа в три раза короче, чем в двоичной системе счисления) и шестнадцатеричная системы счисления (в ней запись числа в четыре раза короче, чем в двоичной).

Так как десятичная система для нас удобна и привычна, все арифмети­ческие действия мы делаем в ней, и преобразование чисел из произвольной недесятичной (q ≠ 10) на основе разложения по степеням q. Преобразование из десятичной в прочие системы счисления производится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.

АЛФАВИТ 2-чной системы счисления: 0 1

АЛФАВИТ 8-ричной системы счисления: 0 1 2 3 4 5 6 7

АЛФАВИТ 10-чной системы счисления: 0 1 2 3 4 5 6 7 8 9

АЛФАВИТ 16-ричной системы счисления: 0 1 2 3 4 5 6 7 8 9 A B C D E F

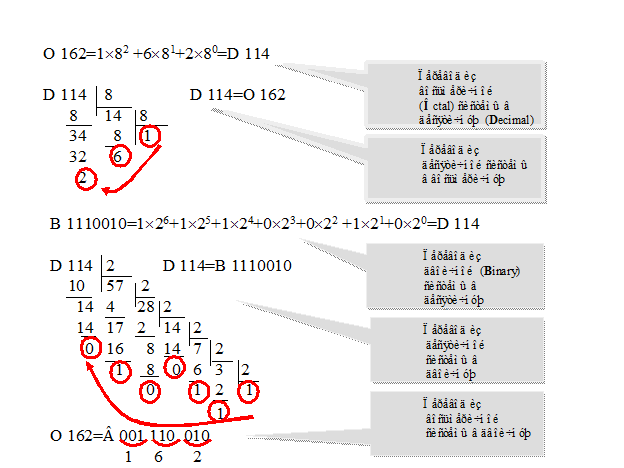
Для перевода числа из десятичной системы счисления в любую другую систему счисления нужно делить «до упора» это число на основание той системы (основание системы – это количество символов в ее алфавите), в которую переводим число, а потом прочесть остатки справа на­лево. Для пе­ревода числа из любой системы счисления в десятичную нужно умножить содержимое каждого разряда на основание системы в степени рав­ной поряд­ковому номеру разряда и всё сложить. Перевод числа из восьмеричной сис­темы в двоичную осуществляется заменой слева направо восьмеричной цифры тремя двоичными цифрами. Перевод числа из двоичной системы счисления в восьмеричную осуще­ствляется заменой справа налево каждой триады двоичных цифр на одну восьмеричную цифру.

Для перевода числа из десятичной системы счисления в любую другую систему счисления можно воспользоваться стандартной программой Каль­кулятор.

Набрав число и щелкнув на одном из переключателей Hex, Dec, Oct или Bin, получим представление этого числа в соответствующей системе.

Как отмечалось, двоичная сис­тема счисле­ния, будучи естественной для ЭВМ, не удобна для восприятия чело­ве­ком. Большое количе­ство разря­дов двоичного числа по сравнению с соответ­ст­вующим десятичным, однооб­раз­ное чередование единиц и нулей является ис­точником ошибок и затруд­нений чтения двоичного числа. Для удобства записи и чтения двоичных чи­сел (но не для работы цифровых вычислительных машин!), необходима бо­лее удоб­ная для записи и чтения система счис­ления. Такими являются сис­темы с ос­нова­нием 2³ = 8 и 2⁴ = 16, т.е. восьмеричная и шестнадцатеричная сис­темы счисления. Названные системы удобны тем, что в них, с одной сто­роны, обеспечивается чрезвычайно лег­кий перевод из двоичной сис­темы (а также обратный перевод), т.к. основание системы – степень числа 2, с дру­гой - со­храняется компактный вид числа. Восьмеричная система широко ис­пользо­валась для записи машин­ных программ в ЭВМ 1 и 2 поколений. В на­стоящее время используется, в ос­нов­ном,

шестнадцатеричная система. Приведем пример соответствия шестна­дца­теричной и двоичной системы:

Пример для тетрад:

0000 = 0; 0001 = 1; 0010 = 2; 0011 = 3; 0100 = 4; 0101 = 5; 0110 = 6; 0111 = 7; 1000 = 8; 1001 = 9; 1010 = A; 1011 = B; 1100 = C; 1101 = D; 1110 = E; 1111 = F.

В ЭВМ используется представление информации в виде «машин­ного слова», длина которого равна некоторому числу бит, характерному для дан­ного типа ЭВМ. В ЭВМ первых поколений использовались ма­шинные слова различной длины, например 45 бит и т.д., то есть не равные це­лому числу байт. В современных компьютерах длина слова обычно 4 или 8 байт (в пер­вых моделях персональных компьютеров было 1 или 2 байта).

Слово в машинной памяти

15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

старший байт младший байт

слово

Дата добавления: 2014-01-11