Решение. 1) Проводим статический анализ системы: создаем эквивалентную схема системы с освобождением конструкции от опорных связей

1) Проводим статический анализ системы: создаем эквивалентную схема системы с освобождением конструкции от опорных связей, которые заменяются силами реакций этих связей, см. рисунок 29,б (при таком простом нагружении заданной горизонтальной силой F в жестких заделках О и В будут возникать только горизонтальные силы реакции связей N_O и N_B); составляем единственно возможное уравнение статического равновесия этой простейшей конструкции (продольную центральную ось стержня обозначим z)

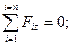конкретно N_O + N_B – F = 0,

в которое входят два неизвестных силовых фактора – опорные реакции N_O и N_B; степень статической неопределимости конструкции: п_с = п_н – п_у = 2 – 1 = 1, где п_н = 2 – количество неизвестных силовых факторов в уравнении статики, п_у = 1 – уравнение статики в данном случае только одно; таким образом, данная система один раз статически неопределима, т. е. вычислить две неизвестных силы из одного уравнения статики невозможно, поэтому необходимо составить одно дополнительное силовое уравнения, в котором должны фигурировать эти неизвестные силы;

2) Осуществляем деформационный анализ конструкции, т. е. рассматриваем ее переход из недеформированного состояния в деформированное; в данном случае общая длина стержня l = const до и после нагружения силой F, изменяются длины участков l_OC и l_CB (участок ОС укорачивается на величину абсолютной продольной деформации Δl_OC, а участок СВ удлиняется на величину Δl_CB, модули этих деформаций равны, т. к. общая длина стержня l = const); таким образом, для данной конструкции получаем уравнение совместности деформаций элементов

Δl_OC = Δl_CB;

3) На основе полученного уравнения совместности деформаций, применяя закон Гука (в форме 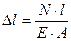), связывающий между собой усилия и деформации, составляем дополнительное силовое уравнение

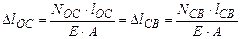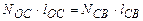или или ,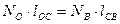

где N_OC и N_CB – внутренние продольные силы в сечениях соответственно участков ОС и СВ, модули которых равны соответственно модулям сил реакций N_O и N_B;

l_OC и l_CB – заданные начальные (до нагружения силой F) длины участков стержня;

4) Раскрываем статическую неопределимости системы, т. е. совместно решаем составленное в п. 1) уравнение статики и в п. 3) дополнительное силовое уравнение с целью вычисления неизвестных сил N_O и N_B в заданной статически неопределимой системе; здесь результаты решения следующие:

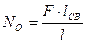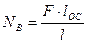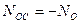; ; (сжатие); 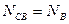(растяжение).

Задача решена.

Контрольные вопросы:

1) Как выбираются допускаемые напряжения (расчетные сопротивления) для расчетов на статическую прочность стержней при центральном растяжении-сжатии: для упруго-пластических материалов; для хрупких материалов?

2) Чем отличаются допускаемые напряжения и расчетные сопротивления материалов?

3) Запишите и объясните условия статической прочности стержней при центральном растяжении-сжатии: для проверочных расчетов; для проектировочных расчетов; для определения допускаемой продольной нагрузки.

4) Запишите и объясните условия жесткости стержней при центральном растяжении-сжатии.

5) Какие конструкции называются статически определимыми системами? Какими методами они рассчитываются?

6) Как проводится статический анализ конструкций, что такое степень статической неопределимости системы и чему она равна для статически определимой конструкции?

7) Какие конструкции называются статически неопределимыми системами? Какова общая методика их расчета?

ГЛОССАРИЙ

	Расчетное напряжение	Settlement pressure
	Допускаемое напряжение	A supposed pressure
	Расчетное сопротивление материала	Settlement resistance of a material
	Условие прочности конструкции	A condition of durability of a design
	Условие жесткости конструкции	A condition of rigidity of a design
	Допускаемая деформация	Supposed deformation
	Статически определимая конструкция (система)	Statically definable design (system)
	Статически неопределимая конструкция (система)	Statically indefinable design (system)
	Уравнение совместности деформаций	The equation of jointness of deformations

Рекомендуемая литература

1. Александров А.В. и др. Сопротивление материалов. Учебник для вузов – М.: Высш. шк., 2001. – 560 с. (с. 63…69; 91…96).

2. Степин П.А. Сопротивление материалов. – М.: Высш. школа, 1983. – 303 с. (с. 42…46; 57…66).

3. Справочник по сопротивлению материалов/Писаренко Г.С. и др. – Киев: Наукова думка, 1988. – 737с. (с. 149…152; 115; 180…182).

Контрольные задания для СРС.

1) Понятие о статически неопределимых системах и методах их расчетов (см. п. 6.8).

2) Общее понятие о методе расчета конструкций по предельным состояниям ([1], с. 91-94).

3) Общее понятие о расчетах конструкций по методу допускаемых напряжений ([1], с. 94-95).

4) Общее понятие о расчетах конструкций по методу разрушающих нагрузок ([1], с. 95-96).

5) Общее понятие о вероятностных методах расчетов конструкций на прочность([1], с. 96-107).

6) Получить конкретные цифровые результаты расчета статически неопределимой системы по рисунку 29,а при исходных данных: F = 100 кН, l = 0,6 м, l_OC = 0,2 м. Построить эпюру внутренних продольных сил N. Определить значение абсолютной продольной деформации участка ОС (Δl_OC), приняв площадь поперечного сечения А = 400 мм² и модуль упругости материала при продольных деформациях 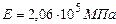(сталь). Проверить статическую прочность стержня, приняв допускаемое напряжение для стали, из которой он изготовлен 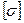= 180 МПа.

Лекция 9. Тема 6. «Центральное растяжение-сжатие прямых жестких стержней»

Цель лекции – рассмотреть основы теории напряженного состояния при одноосном растяжении (сжатии) элементов конструкций с выявлением закономерностей, важных для теории и практики инженерных расчетов и исследований, дать начальные сведения о двухосном и трехосном напряженно-деформированных состояниях упругого тела.

План лекции (курсивом – материалы для СРС)

1. Основы теории напряженного состояния. Внутренние усилия и напряжения в косых сечениях при одноосном растяжении-сжатии стержней.

2. Главные площадки и главные напряжения, экстремальные касательные напряжения.

3. Закон парности (взаимности) касательных напряжений.

4. Понятия о двухосном (плоском) и трехосном (объемном) напряженных состояниях.

5. Обобщенный закон Гука.

Дата добавления: 2014-01-11