Типы бинарных отношений

Введенные выше общие свойства бинарных отношений позво­ляют Формально определить такие их важнейшие типы, как отношения эквивалентности, строгого порядка, нестрогого порядка, доминирования и толерантности. Сущность формального опреде­ления типа отношений сводится к тому, что каждому типу со­поставляется определенная группа свойств. Взаимосвязь этих свойств и типов отношений дана в таб. 1.

Знаки + и – соответственно означают наличие или отсутс­твие того или иного свойства. Знаки + соответствуют свойс­твам, определяющим данный тип отношений, знак ± означает, что это свойство не является обязательным. Нетрудно заметить, что по своей сущности табл. 1 есть таблица отношений между свойствами и типами отношений.

Прокомментируем теперь формально определение типов отношений на понятийной языке.

Таблица 1

Свойства типы отношения	Рефлек- сивность	Антиреф- лексивность	Симмет- ричность	Антисим- метричность	Асиммет- ричность	Транзити- вность
Эквивалентность	+	–	+	–	–	+
Нестрогий порядок	+	–	–	+	–	+
Строгий порядок	_	+	–	+	+	+
Доминирование	–	+	–	+	+	±
Толерантность	+	–	+	–	–	±

Отношение эквивалентности позволяет установить взаимосвязь между словами понятийного языка «одинаковость», «неразличимость», «взаимозаменяемость» и строгими понятиями ТМЯ. Как следует из таблицы 1, бинарное отношение называется эквивалентным, если оно рефлексивно (т.е. каждый элемент эквивалентен самому себе) (а~а), симметрично (т. е. a~b → b~a) и транзитивно (т.е. a~b Ù b~c → a~c).

Важнейшее значение отношения эквивалентности состоит в том, что оно определяет признаки, по который может быть осуществлено разбиение некоторого множества X на непересекающиеся подмножества X₁, …, Х_nÍХ, называемые классами эквивалентности (рис.3). Подмножества X₁, … X_n иногда также называются эталонами. Эталоны могут состоять из ряда элементов x^l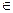X₁. Если же существует множество Y и отображение f:X®Y такое, что всем х¹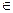Х соответствует только один элемент у₁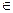Y₁, то говорят, что такое отображение эквивалентно. Это очень важное обстоятельство, связанное с возможностью сжатия описания данных. Так, например, Y₁, может являться именем всех элементов, входящих в класс X₁. Однако, что бы найти конкретные данные в классе X₁, каждому из них следует присваивать свое имя.

Исключение составляет случай, когда задано множество аргументов х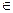Х некоторой функции. Тогда множество значений уÎY этой функции хранить не надо, так как "по имени" этой функции расчетным путем может быть найден любой из элементов у.

Применительно к проблематике баз данных это означает, что вместо хранения массива и его имени можно хранить лишь имя функции, а ее значение получать расчетным путем, т.е. задача поиска данных заменяется расчетной. По современным воззрениям это в ряде случаев может быть целесообразно, хотя совсем недавно такое решение вопроса считалось абсурдным.

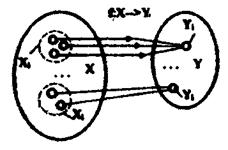
Рис. 3.

Отношение порядка устанавливает, правила следования эле­ментов множества друг за другом. Как это следует из табл. 1. различают отношения строгого и нестрогого порядка. В отношениях нестрогого порядка допускается свойство рефлексивности (равенства) элементов. Это например, означает, что при упорядочении множества вещественных чисел может использоваться знак нестрогого неравенства £, а соответствующая взаимосвязь между элементами записывается как а₁£а_j, которая читается "a_i не следует за a_j" или "а_i предшествует или сов­падает с а_j".

Свойства нестрогого порядка при использовании введенной символики записываются так:

- рефлексивность а£а;

- антисимметричность: (а£b) Ù (b£а) ® а=b;

- транзитивность: (а£b) Ù (b£с) ® а£с.

В отношениях строгого порядка эквивалентность (равенс­тво) элементов исключается. Для обозначения соответствующей взаимосвязи между элементами a_i и а_j используется запись a_i<a_j. которая читается " а_i предшествует а_j”.

Отношение строгого порядка является антирефлексивным, асимметричным и транзитивным. Так как отношение асимметрич­ности следует из антирефлексивности и транзитивности, то от­ношение строгого порядка определяют как любое антирефлексивное и транзитивное. Это записывается следующим образом:

- антирефлексивность: "a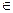A <a,a>ÏP;

- транзитивность: (а<b) Ù (b<с) ® а<с.

Строгий порядок называется совершенным, если отношение определено для двух любых элементов множества.

Если на множестве А задано отношение строгого порядка, то элемент а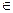A называется минимальным при условии, если не существует b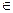A, для которого b<а. Если же элемент а макси­мальный, то не существует b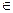А, для которого а<b.

Среди разновидностей строгого порядка важным является древовидный порядок, удовлетворяющий следующим условиям:

- во множестве А существует максимальный элемент, называемый корнем дерева (элемент а₅, на рис. 4):

- справедливо утверждение (а<b) Ù (а<с) ® (b<c) Ú (c<b), где символ Ú дизъюнкция, соответствующая союзу "ИЛИ". Последнее условие означает, что элементы b и с несравнимы.

Древовидные порядки находят широкое применение при опи­сании структурных схем автоматизированных систем сбора в об­работки информации (АССОИ), а также в иерархических струк­турах описания данных. При этом аналогом дерева может быть таблица связанностей файлов, в которой помещены соответствующиевзаимные ссылки.

Отношение доминирования описывает взаимосвязь между элементами множества а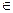А и b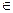А, когда относительно них из­вестно, что один из них, например а, превосходит в чем-то элемент b. Условие доминирования записывается так: а>b (а до­минирует над b). Определяющим в отношении доминирования является асимметричность. По этой же причине отношение доминирования должно быть антирефлексивно. Однако, оно может и не быть транзитивным. Так, доминирующим на рис. 4 является элемент a₅.

Отношение толерантности t на множестве A удовлетворяет свойствам рефлексивности и симметричности, но свойство тран­зитивности не является обязательным. Поэтому отношение эквивалентности рассматривается как частный случай отношения то­лерантности.

Отношение толерантности используется для описания мно­гих прикладных задач, стоящих перед ACCOИ. Пусть, например, имеется М={a₁, a₂, …, a_n} множество объектов и H={b₁, b₂,... b_n} - множество признаков. Каждому элементу а_iÎM соответствует подмножество признаков H_iÍ H. В задачах рас­познавания образов идентификация состояния и т.н. сходство между объектами а_i и а_j, определяется толерантностью соот­ветствующих им подмножеств (Н_i, Н_j,)ÍН, т.е. выполнением ус­ловия H_iÇН_j¹Æ. При этом о сходстве (или различии) между объектами судят по толерантности элементов в множестве признаков.

Рис. 4.

Дата добавления: 2014-01-11