Общие свойства бинарных отношений

Введение.

Учебные вопросы (основная часть):

1. Общие свойства отношений.

2. Типы бинарных отношений.

Литература:

Основная:

1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2002. – 304с.: ил. (Рек. МО)

2. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 215с.: ил.(Рек. МО)

Дополнительная:

3. Кузнецов О.П. и др. Дискретная математика. - М.: Высшая школа, 1986. – 321с.: ил. (Рек. МО)

Учебно-материальное обеспечение:

1. Наглядные пособия: электронный конспект лекций

2. Технические средства обучения: интерактивная доска

К общим свойствам бинарных отношений относятся свойства рефлексивности, антирефлексивности, симметричности, асимметричности, антисимметричности и транзитивности. Каждое из этих свойств может быть описано на теоретико-множественном языке (ТМЯ), языке графов, матриц и пр. Одной из наиболее наглядных форм представления свойств отношений является язык графов, которым мы будем пользоваться наряду с ТМЯ.

Бинарное отношение называется рефлексивным, если для всех аÎА кортеж <a, a>ÎP.

Если ввести понятие множества элементов D таким образом, что

D={<a, a>|aÎA).

то это множество называется диагональю декартова квадрата A´А. Следовательно, отношение рефлексивно, если

DÍP

На языке графов это означает, что каждая вершина графа отношений (рис.1.а) имеет петлю, на языке матриц - в реф­лексивном отношении все элементы, стоящие, на ее главной диагонали, есть единицы.

Бинарное отношение антирефлексивно, если отношение Р не содержит диагональ, т.е.

РÇD=Æ

Граф антирефлексивного отношения (рис.1.б) не содер­жит петель, а матрица отношений - единиц на главной диагона­ли.

Наконец, бывают отношения, которые нельзя отнести как к рефлексивным, так и к антирефлексивным (рис.1.в).

Бинарное отношение называется симметричн ым, если для любой пары <а, b>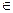Р выполняется условие <b, а>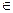Р. Это озна­чает, что

Р^-1=P.

На языке графов при инверсии отношения должны меняться направления стрелок, а в матрицах должно осуществляться их транспонирование. Следовательно, чтобы отношение было сим­метричным, необходимо, чтобы две любые вершины его графа или имели только петли, или не были соединены друг с другом, или же чтобы их связывали между собой две стрелки противоположного направления (рис. 1.г).

Бинарное отношение называется антисимметричным, если

PÇP^-1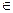D

Это означает, что одновременное выполнение условий <а,b>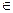Р, <b,a>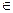P возможно лишь для диагональных элементов отношения. Поэтому в графе отношения могут быть петли, но не могут быть вершины, связанные противоположно направленными стрелками.

Бинарное отношение называется асимметричным, если

PÇP^-1=Æ

Граф асимметричного отношения обладает теми же свойс­твами, что и граф антисимметричного отношения, но кроме то­го, еще и не содержит петель (рис. 1.б). Это означает, что матрица отношений имеет нулевые диагональные элементы и не содержит ни одной пары элементов, симметричных относительно главной диагонали.

Бинарное отношение называется транзитивным, если

[<a, b>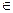P] Ù [<b, c>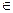P] → <a, c>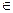P,

здесь Ù - знак конъюнкции, соответствующий союзу "И"; → – знак импликации, соответствующий обороту "если ….,то". В пе­реводе на понятийный язык эта запись звучит так: "если пары <а, b> и <b, c> являются элементами множества некоторого отношения Р и при этом пара <а, с> также является элементом Р, то отношение называется транзитивным". Кратко эта запись может быть определена так:

Р·Р = Р.

т.е. отношение Р·Р является композицией отношения Р самим с собой. На языке графов это может быть проинтерпретировано следующим образом: если в графе отношения существует такая вершина а_к (рис.2.а), которая соединена соответствующими стрелками с вершинами a_i и а_j, то последние также должны быть соединены между собой стрелкой соответствующего направления. Это правило распространяется на произвольное число точек а_k. Пример транзитивного отношения, представленного в виде графа отношений, и его упрощенное изображение представлены соот­ветственно на рис. 2. б, в.

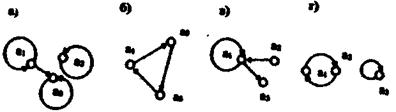
Рис. 1

Рис. 2.

Дата добавления: 2014-01-11