Микросостояние. Вероятность. Средние значения

Основу статистической физики составляет теория вероятностей

ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

СТАТИСТИЧЕСКАЯ ФИЗИКА

9.1. Микросостояние. Вероятность. Средние значения

9.2. Распределение Максвелла.

9.3. Распределение молекул по модулям скорости

9.4. Формула Максвелла в приведенном виде

9.5. Распределение по энергиям молекул

Статистическая физика — это раздел физики, в котором

1. изучают свойства макросистем, исходя из

· индивидуальных свойств составляющих макросистему частиц

· и взаимодействий между ними.

2. оперирует со средними значениями параметров очень большого числа частиц Т.к. описание движения каждой частицы макросистемы (а их порядка 10²² - 10²³) — задача совершенно немыслимая.

3. Колоссальное число частиц в макросистеме приводит, несмотря на очевидный хаос, к появлению новых, статистических закономерностей. Их изучение и делает возможным описание макросистем на основе сведений о свойствах отдельных частиц.

О вероятности.. Исходные понятия этой теории — событие и вероятность.

Событие — это, например,

- выпадение одного из шести номеров при бросании игрального кубика.

- Или при измерении скорости молекул газа: разбив возможные значения скоростей на отдельные интервалы 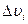(i = 1, 2,...) и обнаружив, что скорость молекулы попала в i-й интервал, мы говорим об i-м событии.

В дальнейшем нас будут интересовать лишь такие события, которые являются:

1) случайными, т. е. событиями, условия наступления которых по тем или иным причинам неизвестны и которые поэтому нельзя заранее с уверенностью предсказать;

2) равновозможными или равновероятными — для которых нет никаких оснований ожидать, что при испытаниях они будут вести себя по-разному (например, при бросании игрального кубика или монеты, но никак не бутерброда с маслом).

Вероятность данного случайного события характеризуется кратностью его повторения. Если в N случаях i-e событие происходит N_t раз, то

вероятностью Pi этого события называют величину

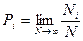
Так как на практике N всегда конечно, то для вычисления вероятности стараются, чтобы N и N_i были достаточно большими. Тогда можно считать, что

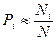
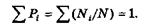
Ясно, что сумма вероятностей всех возможных результатов измерений равна единице:

Вычисление вероятностей сложных событий.

Рассмотрим две основные теоремы: о сложении и умножении вероятностей на примере игрального кубика.

1. Теорема сложения вероятностей.

Если в результате N бросаний кубика в N_i случаях выпадет число i, а в N_k случаях — k, то вероятность выпадения i или k равна

Это значит, что при бросании кубика вероятность выпадения, скажем, 2 или 5 равна Р = ¹/₆ + ¹/₆ = ¹/₃.

В общем случае эта теорема утверждает: вероятности несовместимых событий складываются. Пример. При бросании игрального кубика вероятность:

а) выпадения четной цифры равна ¹/₆ + ¹/₆ + ¹/₆ = ¹/₂

б) того, что не выпадет 2, равна ⁵/₆

2. Теорема умножения вероятностей.

Найдем вероятность того, что при двух бросаниях кубика выпадет последовательно i и k. Рассмотрим N двойных бросаний.

Пусть первый из каждой пары бросков дал i в N_t случаях (так что .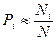

Теперь выделим из этих N_i случаев те N_k событий, когда второй бросок кубика давал k (так что ).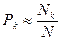

Тогда искомая вероятность

Значит, вероятность того, что при двух бросаниях кубика выпадут, допустим, сначала 2, а затем 5, равна ¹/₆ • ¹/₆ = ¹/₃₆-

В общем случае теорема умножения вероятностей утвержда­ет: вероятность совмещения двух или нескольких событий равна произведению вероятностей каждого их них в отдельно­сти.

Пример. Вероятность того, что при двух бросаниях кубика:

а) выпадут две 5, равна ¹/₆ • ¹/₆ = ¹/₃₆

б) не выпадет ни одной 5, равна ⁵/₆ • ⁵/₆ = ²⁵/₃₆;

в) выпадет одна 5, равна (¹/₆ • ⁵/₆) + (¹/₆ • ⁵/₆) = ¹⁰/₃₆

Заметим, что Р_а + Р₆ + Р_в = 1, как и должно быть.

Для исследования и количественного описания статистических закономерностей вводят, в статистической физике, многомерное пространство, которое называется фазовым пространством.

Это такое пространство, в котором в качестве координатных осей выбираются координаты X_i и импульсы p_i частиц, входящих в макроскопическую систему А.

· Если в систему входит N частиц, то размерность фазового пространства 3 N +3 N =6 N

(3 N координатных осей - проекции координат всех частиц системы А,

3 N координатных осей - проекции импульсов).

·

P     dP a dx   х Рис.1.     Рис.1 x

Рис.1. Если система характеризуется одной степенью свободы, то фазовое пространство двухмерно

- Точка а фазового пространства характеризует микросостояние системы А (т.е. совокупность всех координат X_i и импульсов p_i всех частиц системы А) в некоторый момент времени и называется фазовой точкой.

- кривая на рис.1. Из-за взаимодействия частиц между собой и с окружающим пространством положение фазовой точки а в следующий момент времени изменится, т.е. фазовая точка сместится по фазовой траектории

Если через каждые 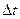измерять X_i и p_i частиц системы А и наносить точку в фазовом пространстве, то спустя большие время Т в фазовом пространстве получается облако точек.

Эти точки изображают возможные микросостояния системы А, совместимые с данным макросостоянием. За время Т система А побывает во всех возможных микросостояниях, которые совместимы с данным макросостоянием.

Дата добавления: 2014-01-11