Распределение Максвелла. Закон распределения по скоростям молекул газа, находящегося в термодинамическом равновесии, был найден Максвеллом (1859)

Закон распределения по скоростям молекул газа, находящегося в термодинамическом равновесии, был найден Максвеллом (1859).

Рассмотрим физический смысл закона Максвелла и некоторых его следствий.

· Представим себе

- пространство скоростей с прямоугольными координатными осями, по которым будем откладывать значения проекций отдельных молекул.

- Тогда скорости каждой молекулы будет соответствовать точка в этом пространстве — конец вектора .

- Из-за столкновений молекул положения точек будут стремительно меняться, но их распределение в целом будет оставаться неизменным, поскольку макросистема находится в термодинамическом равновесии.

Рис.3.

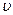Вследствие равноправности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Поэтому плотность точек может зависеть только от модуля скорости (но не от ).

· Пусть макросистема (газ) содержит N молекул.

· Выделим в некоторой точке — конце вектора — малый объем

(рис. 3, где ось 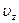направлена на нас).

Относительное число точек (молекул) в этом объеме, или другими словами,

1. вероятность dP того, что скорость молекулы, т.е. конец вектора , попадет в этот объем, можно записать так:

, (2)

где имеет смысл объемной плотности вероятности.

3. Вероятность же того, что молекула (точка) будет иметь проекции скорости в интервале (),

есть , (3)

где — функция распределения по .

Выражение (3) — это по существу интеграл (2) по и 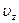, т.е. относительное число молекул (точек) в тонком плоском слое от до + d .

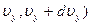3. Вероятности того, что молекула имеет проекции скорости в интервалах (,+d), (и (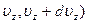) являются независимыми, поэтому в соответствии с теоремой об умножения вероятностей независимых событий можно записать

(4)

Из соображения равноправия осей , и 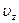ясно, что функции φ должны одинаковым образом зависеть от соответствующих проекций скоростей. Сопоставив (4) с (2), находим

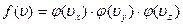. (5)

После преобразований (с учетом условия нормировки) получаем

,

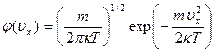аналогичный вид имеют функци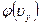и и .

И тогда согласно (5). (6)

рис. 4. График функции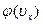

Он совпадает с гауссовой кривой погрешностей. Площадь тонированной полоски на рис. 4 — это вероятность того, что проекция скорости молекулы лежит в интервале (,+ d ).

Функция (6) нормирована на единицу,

т.е. площадь под кривой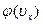

Интегрирование в пределах от -∞ до +∞ не означает, что в газе есть молекулы с такими большими скоростями. Это следует рассматривать только как вычислительный прием. Молекул с весьма большими скоростями очень мало, и они практически не вносят никакого вклада в нормировочный интеграл. Это и позволяет записывать такие пределы.

Дата добавления: 2014-01-11