Барометрическая формула

Умножив обе части распределения Больцмана на kT,

получим со­гласно основному уравнению МКТ, что давление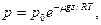

где 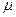— молярная масса, R — универсальная газовая постоянная.

Это так называемая барометрическая формула.

Она строго спра­ведлива для идеального газа, температура которого не зави­сит от высоты (изотермическая атмосфера).

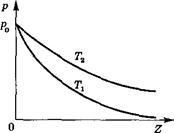
На рис. 11 пока­заны два графика зависимости давления от высоты z при разных температурах 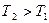. Следует обратить внимание на то, что в отличие от распределений n(z), кривые p(z) на рис. 11 начинаются в одной точке независимо от температуры.

Это не случайно и имеет простое объяснение.

Рис.11

Рассмотрим, как ведет себя центр масс газа в поле тяжести.

При анализе ситуации, изображенной на рис. 11, мы приходим к выводу, что

в результате повышения температуры от 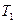до 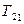центр масс газа перемещается вверх.

Возникает вопрос: под действием какой внешней силы?

На первый взгляд вроде ничего не изменилось — ни сила тяжести, ни сила реакции со стороны поверхности Земли (ведь давление 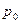осталось прежним).

На самом же деле в процессе нагревания газа равновесие нарушается, вторая сила оказывается большей по модулю. Она направлена вверх и вызывает перемещение центра масс.

Представим барометрическую формулу в виде ,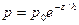

где 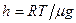— это высота, на которой давление убывает в е раз.

Значение h играет роль характерной толщины атмосферы.

При 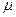= 20 г/моль и Т = 280 К величина h = 8 км.

По сравнению с радиусом Земли атмосфера — тонкая пленочка (что и позволяет при получении барометрической формулы считать ускорение g не зависящим от высоты).

Вычислим число молекул с помощью функции распределения Больцмана.

· Возьмем на поверхности Земли площадку с площадью S = 1

· и рассмотрим столб воздуха над этой площадкой.

· В слое толщиной dz на высоте z находится число молекул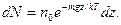

· Интегрируя это выражение по z от 0 до ∞, находим полное число молекул N столбе: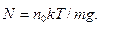

· Затем умножим N на массу т одной молекулы и на площадь поверхности Земли 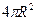. В результате найдем, что масса М атмосферы

.

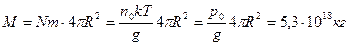Эту задачу можно решить и проще, рассуждая так.

Поскольку атмосфера Земли в целом находится в равновесии, то можно считать, что сила тяжести, действующая на газ в каждом вертикальном столбе единичного сечения, уравновешивается силой реакции со стороны поверхности Земли, т.е. давлением

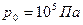(1 атм).

Умножив 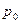на площадь поверхности Земли, получим Mg, где М — искомая масса.

Отсюда М = 5,3 • 10¹⁸ кг.

Строго говоря, атмосфера Земли не является равновесной.

Атмосфера непрерывно рассеивается, хотя для Земли этот процесс идет очень медленно. Рассеивание обусловлено тем, что в процессах соударения молекул в верхних слоях атмосферы неизбежно возникают молекулы, скорости которых оказываются больше второй космической. И таким молекулам иногда «удается» без столкновений покинуть атмосферу Земли. За все время существования Земля потеряла очень малую часть своей атмосферы.

Из распределения Больцмана возникает следующий «парадокс»: почему в поле тяжести при движении молекул

· вверх их кинетическая энергия уменьшается, а температура остается прежней, т.е. средняя кинетическая энергия не меняется,

· а при движении вниз кинетическая энергия всех молекул увеличивается, а средняя их энергия остается той же?

Этот «парадокс» был разъяснен уже Максвеллом. При движении

· вверх молекулы действительно замедляются, но при этом наиболее медленные молекулы выбывают из потока частиц.

· вниз, наоборот, молекулы не только ускоряются, но одновременно их поток пополняется более медленными молекулами. В результате средняя скорость теплового движения молекул остается неизменной.

Дата добавления: 2014-01-11