Группы. Определение и основные свойства

Определение 4. Алгебра G=<A, {*,^-1}> типа <2,1> называется группой, если ее операции удовлетворяют следующим аксиомам:

1) (x*y)*z=x*(y*z) (ассоциативность);

2) (у^-1*у)*х=х=х*(у*у^-1) (существование обратного элемента).

Операция * обычно называется умножением. Если она ком­мутативна, то иногда ее называют сложением. Могут использо­ваться и специальные названия, отвечающие ее содержанию. Обычно символ операции * опускают и записывают вместо а*b просто ab. Далее это будет использоваться.

Из определения 4 сразу следует, что в группе су­ществует, и притом единственный, элемент, являющийся единичным (единицей группы). Действительно, из аксиомы 2 следует (у^-1*у)*х=х, т.е. (у^-1у)=е - единичный элемент. Если предполо­жить, что существует еще один единичный элемент е', то полу­чим е=ее'=е'.

Пример 4. Рассмотрим полугруппу из примера 1. Введем в этой системе тождественное отображение е:A®A, такое, что е(а)=а для любого аÎA. Очевидно, что это отображение относительно операции композиции отображений иг­рает роль единичного элемента. Множество Ф_А всех биективных отображений произвольного множества А на себя замкнуто отно­сительно операции композиции и тождественное отображение входит в него. Далее, для каждого биективного отображения jÎФ_А существует и притом единственное отображение j^-1, ко­торое является обратным по отношению к j, т.е. j^-1j=jj^-1.

Таким образом, полугруппа <Ф_А,{*}> всех биективных отоб­ражений j:A®A, является группой, если в нее ввести дополни­тельно операцию ^-1, так как в Ф_А существует единичный эле­мент и каждый элемент jÎФ_А имеет обратный j^-1.

Группа всех отображений непустого множества А в себя называется симметрической группой. Эта группа имеет большое значение в теории групп.

Пример 5. Пусть А={1,2,3} - трехэлементное мно­жество. Рассмотрим симметрическую группу всех биективных отображений множества А в себя (см. пример 4). Эта группа называется группой подстановок s₃. Перечислим все возможные отображения такого вида, записывая их, как это принято в алгебре, в виде двух строк, первая из которых от­носится к аргументам, а вторая - к образам отображений:

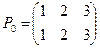
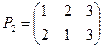
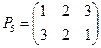
Число различных подстановок в s, равно 3! (числу всех перестановок множества из трех элементов), так что Р₀-Р₅ исчерпы­вает все возможные биективные отображения j:A®A.

Композиция (произведение) подстановок определяется по следующему, очевидному из примера, правилу:

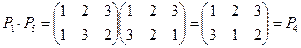
Очевидно, что роль единичного элемента в множестве подстановок играет тождественная подстановка Р₀.

Для всех подстановок s₃ имеет место таблица произведе­ний (табл. 2.), в чем можно убедиться самостоятельно.

На основании табл.2. можно легко найти для любого эле­мента P_i обратный ему. Очевидно, таковым является элемент, который при умножении на Р_i дает тождественную подстановку P₀. Перечислим обратные элементы для каждой из подстановок:

P₀^-1=P₀; P₁^-1=P₁; P₂^-1=P₂;

P₃^-1=P₄; P₄^-1=P₃; P₅^-1=P₅;

Таким образом, все элементы, кроме Р₃, Р₄ являются об­ратными сами себе.

Таблица 2.

Первый мно­житель	Второй множитель
Р0	Р1	Р2	Р3	Р4	Р5
Р0	Р0	Р1	Р2	Р3	Р4	Р5
Р1	Р1	Р1	Р3	Р2	Р5	Р4
Р2	Р2	Р4	Р0	Р5	Р1	Р3
Р3	Р3	Р5	Р1	Р4	Р0	Р2
Р4	Р4	Р2	Р5	Р0	Р3	Р1
Р5	Р5	Р3	Р4	Р1	Р2	Р0

Итак, в множестве подставок s₃ удовлетворены все акси­омы групп, поэтому s₃=<{Р_i},{*,^-1}> является группой относи­тельно операции композиции (произведения).

Определение 5. Подмножество Н группы G называет­ся подгруппой, если оно замкнуто относительно групповой опе­рации (непусто и вместе с любыми двумя элементами а,bÎН со­держит ab), а также вместе с любым аÎН содержит и обратный ему элемент а^-1.

Из определения вытекает, что любая подгруппа содержит единичный элемент подгруппы, так как из замкнутости группо­вой операции следует, что а^-1а=aа^-1=e. т.е. еÎН.

Дата добавления: 2014-01-11