Проблема кодирования состояний асинхронных конечных автоматов

Построив таблицу переходов, которая удовлетворительно описывает желаемую последовательностную функцию, мы должны на следующем этапе синтеза выбрать конечное множество двоичных внутренних переменных и приписать каждой строке таблицы переходов одно или несколько состояний этих переменных. После этого непосредственной задачей является построение таблиц истинности (логических последовательностей), определяющих значения выходов схемы и следующие значения внутренних переменных как функции текущих значений входов и внутренних переменных.

Для того чтобы однозначно закодировать каждую строку таблицы переходов, число внутренних переменных 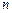должно удовлетворять условию

,

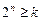где 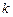– число строк таблицы.

Удобно записать это условие в виде

,

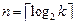где 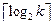– ближайшее наибольшее целое число.

Каждому внутреннему состоянию ставится в соответствие определённая комбинация 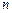внутренних переменных. Общее число таких комбинаций равно 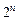. В простейшем случае каждому состоянию можно сопоставить его двоичный эквивалент. Но при таком способе кодирования при некоторых переходах могут изменять своё значение сразу несколько внутренних переменных.

Ситуация, при которой в процессе перехода возможны изменения более чем одной внутренней переменной, называется условием состязания. Если правильное поведение схемы зависит от результата состязания, то такое состязание называется критическим. Если же поведение системы совпадает с поведением, задаваемым таблицей переходов независимо от результата состязания, то такое состязание называется некритическим.

Поэтому проблема кодирования состояний (строк) заключается в приписывании строкам таблицы переходов комбинации значений двоичных внутренних переменных таким образом, чтобы все внутренние переходы успешно завершались независимо от относительных значений задержек в цепях внутренних переменных (то есть необходимо устранить критические состязания).

Один из методов устранения критических состязаний – соседнее кодирование, при котором на всех возможных переходах меняется только одна внутренняя переменная.

Вернёмся к уже рассмотренной нами таблице переходов счётчика-делителя на 2 (табл. 5).

Переход из состояния 3 (11) в состояние 0 (00) содержит условие критического состязания (рис. 11).

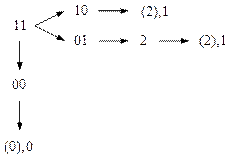
Рис. 11

Указанный переход возможен, если задержки формирования сигналов, соответствующих внутренним переменным, совершенно одинаковы. В случае неодновременного изменения состояния внутренних переменных алгоритм функционирования автомата нарушается (происходит переход из состояния 3 в состояние 2).

Для устранения критических состязаний необходимо иначе закодировать внутренние состояния автомата (табл. 19).

Таблица 19

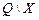
	(0),0	1,*
	3,1	(1),1
	0,0	(2),0
	(3),1	2,*

Все переходы в табл. 19 являются соседними (0 – 1 – 3 – 2 – 0 и т. д.), то есть на каждом переходе изменяется только одна внутренняя переменная и, следовательно, отсутствуют критические состязания.

Дата добавления: 2014-01-11