Метод соединяющих строк

МЕТОДЫ ПРОТИВОГОНОЧНОГО КОДИРОВАНИЯ

Рассмотрим пример противогоночного кодирования для счётчика-делителя на 3, описываемого таблицей переходов 6.

Выпишем из указанной таблицы множества всех возможных переходов из всех состояний:

из состояния 0: – (0, 1, 5);

из состояния 1: – (1, 0, 2);

из состояния 2: – (2, 1,3);

из состояния 3: – (3, 2, 4);

из состояния 4: – (4, 3, 5);

из состояния 5: – (5, 0, 4).

Постараемся закодировать состояния автомата таким образом, чтобы все переходы были соседними, не увеличивая при этом количество внутренних переменных.

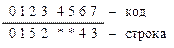
Построим новую таблицу переходов с учётом введённой кодировки состояний рассматриваемого автомата.

Таблица 20

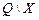
			Строка
	(0),0	1,*
	3,1	(1),1
	0,0	(2),0
	(3),1	7,1
	*	*
	*	*
	(6),0	2,0
	6,*	(7),1

Все переходы в построенной таким образом таблице являются соседними, то есть на каждом переходе меняется только одна внутренняя переменная:

0 – 1 – 3 – 7 – 6 – 2 – 0 – и т. д.

В сложных автоматах соседними переходы часто сделать невозможно, поэтому в таблицу переходов добавляются промежуточные состояния (строки) через которые осуществляется необходимый переход. Такие строки называются соединяющими.

В качестве примера рассмотрим автомат, заданный табл. 21.

Таблица 21

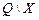
	(0)		(0)
		(1)	*	(1)
		(2)	*	(2)
	(3)		*	(3)
		(4)	*
	(5)		(5)

Выпишем множества всех возможных переходов из всех состояний:

из состояния 0: – (0, 1, 2);

из состояния 1: – (1, 0, 3, 4);

из состояния 2: – (2, 0, 5);

из состояния 3: – (3, 1, 4, 5);

из состояния 4: – (4, 1, 3, 5);

из состояния 5: – (5, 2, 3, 4).

Постараемся закодировать состояния автомата таким образом, чтобы все переходы были соседними. Для этого необходимо добавить ещё одну внутреннюю переменную и дополнительные соединяющие строки.

Начнём кодирование с одного из максимальных множеств – (3, 1, 4, 5). Присвоим состоянию 3 двоичный код (0000), а состоянию 1 – код (0010). При этом переход из состояния 3 в состояние 1 (или наоборот, из состояния 1 в состояние 3) будет соседним:

Для того, чтобы сделать соседними остальные переходы их этого множества, необходимо ввести промежуточное состояние с кодом (0001):

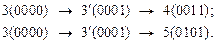
Для множества (4, 1, 3, 5) новые переходы можно представить следующим образом:

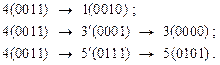
Для множества (5, 2, 3, 4) переходы из состояния 5 в состояния 3 и 4 уже рассмотрены выше:

Из множества (1, 0, 3, 4) остался нерассмотренным только один переход – из состояния 1 в состояние 0. Для его осуществления необходимо добавить три промежуточных состояния:

Построим новую таблицу с учётом введённой перекодировки состояний автомата (табл. 22). В указанной таблице все переходы являются соседними (то есть при переходе из состояния в состояние меняется лишь одна внутренняя переменная).

Таблица 22

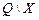
					Строка
	(0)		*	(0)
	*		*
		(2)	*	(2)
		(3)	*
	(4)		(4)
	(5)		(5)
		(6)	*	(6)
			*	*
	*		*	*
	*	*	*	*
	*		*	*
	*	*	*	*
	*		*	*
	*	*	*	*
	*	*	*	*
	*	*	*	*

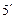
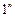
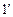
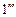
Рассмотрим ещё один пример кодирования состояний автомата методом соединяющих строк. Исходная таблица переходов задана в виде табл. 23.

Таблица 23

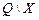
		(0)	(0)	(0)
	(1)		(1)
		(2)		(2)
		(3)		(3)
	(4)		(4)
		(5)	(5)

Выпишем множества всех возможных переходов из всех состояний:

из состояния 0: – (0, 1, 4);

из состояния 1: – (1,0, 2, 3, 5);

из состояния 2: – (2, 1, 5, 4);

из состояния 3: – (3, 1, 4);

из состояния 4: – (4, 0, 2, 3);

из состояния 5: – (5, 1, 2).

Постараемся закодировать состояния автомата таким образом, чтобы все переходы были соседними и попытаемся сделать это без добавления ещё одной внутренней переменной.

Начнём кодирование с максимального множества (1, 2, 3, 5).

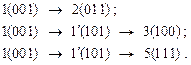
Для множества (2, 1, 5, 4) переход из состояния 2 в состояние 1 уже рассмотрен. Чтобы сделать переходы в состояния 5 и 4 соседними, необходимо присвоить им коды (111) и (010):

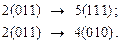
Для множества (3, 1, 4) остался нерассмотренным переход из состояния 3 в состояние 4:

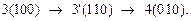
Остальные переходы синтезируемого автомата являются соседними или уже рассмотрены выше.

Построим новую таблицу с учётом введённой перекодировки состояний автомата (табл. 24).

Таблица 24

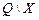
					Строка
		(0)	(0)	(0)
	(1)		(1)
	(2)		(2)
		(3)		(3)
		(4)		(4)
		*	*	*
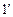
		(7)	(7)

Состояния рассмотренного выше автомата можно закодировать иначе. Выберем одну из максимальных групп (1, 2, 3, 5). В этой группе содержатся кодовые комбинации, которые должны иметь соседние коды. Закодируем состояние 1 комбинацией (000).

Поскольку код состояний рассматриваемого автомата трёхэлементный, в нём имеется только три соседних комбинации. Чтобы увеличить число возможных соседних комбинаций введём дополнительное состояние 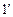, которому можно сопоставить любую кодовую комбинацию, например (001). Остальным состояниям рассматриваемого множества сопоставим следующие кодовые комбинации:

2 – (011);

3 – (100);

5 – (101).

Переходы в рассматриваемом множестве можно осуществить следующим образом:

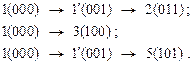
Для нерассмотренных выше переходов из множества (2, 1, 5, 4):

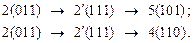
Состоянию 4 сопоставим кодовую комбинацию (110), а состоянию 0 – кодовую комбинацию (010). При этом для множеств (3, 1, 4), (4, 0, 2, 3) и (5, 1, 2) все нерассмотренные выше переходы будут являться соседними.

С учётом введённой перекодировки состояний автомата таблица переходов рассматриваемого автомата будет иметь вид табл. 25.

Таблица 25

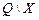
					Строка
	(0)		(0)
			*	*
		(2)	(2)	(2)
		(3)		(3)
		(4)		(4)
		(5)	(5)
	(6)		(6)
	*

Существует целый ряд подобных методов, позволяющих устранить критические состязания за счёт введения дополнительных строк (состояний внутренних переменных). Недостатком указанных методов является более низкое быстродействие АП за счёт более длинных переходов (через промежуточные состояния).

Дата добавления: 2014-01-11