Замена переменных в определённом интеграле

Дифференцирование определённого интеграла, пределы которого дифференцируемые функции.

Вспоминая цепное правило дифференцирования сложной функции, можно написать следующую формулу:. D▲.

Пусть f Î R _{[ a , b ]} и на промежутке x Î[ a, b ] рассматривается . Кроме того, пусть задана функция x = j(t) t Î[a, b], причем j(a) = a, j(b) = b

и функция 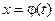строго монотонна и непрерывно дифференцируема на промежутке 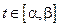. Тогда справедлива формула, именуемая формулой замены переменной в определенном интеграле:

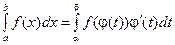. D▲.

На иллюстрации сделана попытка пояснить необходимость монотонности функции x = j(t).

§. Примеры.

1°. Найти .

а). Формальное применение формулы Ньютона–Лейбница дает:

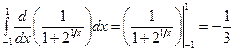, что само по себе удивительно, ибо интеграл от неотрицательной функции оказался отрицательным.

б). Давайте более аккуратно подойдем к нахождению первообразной функции. Для этого найдем первообразную отдельно для x больших и для x меньших нуля.

Получим для 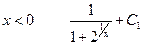, и для . Чтобы найти первообразную на всем промежутке надо потребовать чтобы найденная первообразная была непрерывна, т.е. чтобы 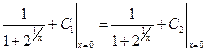Þ . Значит первообразная подынтегральной функции на промежутке имеет вид: и теперь применение формулы Ньютона– Лейбница дает правильный результат .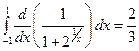

2°. 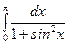. Формально выполняя замену переменной получим что , что очевидно неверно. Для получения правильного результата необходимо учесть, что функция разрывна при 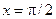и следовало бы написать:

, однако на этом пути нас ожидает еще одна неприятность принципиального порядка. Идея определенного интеграла не может быть реализована для бесконечных промежутков интегрирования. Здесь мы вторгаемся в область несобственных интегралов, которые будут рассмотрены несколько позже.

Приведенные два примера показывают что, и при применении формулы Ньютона –Лейбница и при замене переменной в определенном интеграле следует быть очень осторожным.

§. Формула интегрирования по частям

Дата добавления: 2014-01-11