Вычисление моментов и координат центра масс

Вспомним что, статический момент конечной системы материальных точек с массами и радиус-векторами находится по формуле: . Радиус-вектор центра масс будет равен

, где .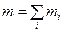

Тогда, если (x, y, z) – декартовы координаты, а 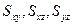- статические моменты системы материальных точек относительно координатных плоскостей соответственно, то , , .

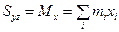А для координат центра масс имеем: ; ; .

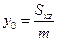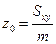Для точек лежащих в одной плоскости с декартовыми координатами (x, y), если обозначить статические моменты относительно осей Ox и Oy получим формулы:

; .

И для центра масс, соответственно: ; .

Для системы точек, лежащих в плоскости можно говорить и о моментах k ^го порядка

, .

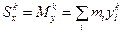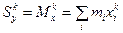При этом ясно, что масса системы точек это момент нулевого порядка, а статические моменты это моменты первого порядка. Моменты второго порядка называются моментами инерции.

Момент инерции системы материальных точек относительно некоторой оси определяется равенством: 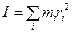, где – расстояния от точек системы до соответствующих осей.

При применении определенного интеграла к вычислению моментов тела разбиваются на тонкие слои из точек «равноудаленных» от соответствующих плоскостей (или осей), и каждый такой слой рассматривается как единое целое и…

Примеры:

1. Найти статический момент эллипса относительно касательной к эллипсу в его «вершине», если эллипс однороден (плотностью 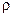). Уравнение эллипса: (рис. б)

Разрежем эллипс на элементарные полоски параллельные оси ординат. Т.к. полоски достаточно узкие, можно считать, что все точки элементарной полоски находятся на одинаковом расстоянии 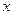от оси ординат. Площадь элементарной полоски, в таком предположении, равна 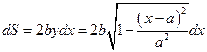. Умножая площадь на плотность, получим массу элементарной полоски ; Расстояние от элементарной полости до оси Oy: .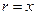

Тогда для статического момента эллиптической пластинки относительно прямой, проходящей через его вершину, параллельно одной из осей (в нашем случае – оси ординат) получаем:

.

Примечание: плотность может даже зависеть от х: ρ=ρ(х), но не от y.

2. Найти момент инерции однородного цилиндра относительно его оси (рис. а).

Разобьём цилиндр на отдельные тонкостенные цилиндры. Объём и масса такого тонкостенного цилиндра (кстати, ρ – может зависеть от расстояния до оси) и соответственно момент инерции .

3. Найти момент инерции однородного витка винтовой линии относительно его оси (рис. в).

Уравнение винтовой линии: . Если взять элементарный отрезок винтовой линии, то его длина равна , масса, соответственно 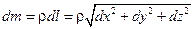и, учитывая, что расстояние до оси равно , получим формулу для момента инерции: =

= = = .

Дата добавления: 2014-01-11