Абсолютная сходимость. Критерий Коши сходимости несобственного интеграла

Критерий Коши сходимости несобственного интеграла.

Рассмотрим несобственный интеграл с одной особой точкой ω на конце промежутка интегрирования. Интеграл 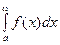сходится, тогда и только тогда, когда

.

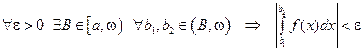D Это, собственно говоря, критерий Коши для того, чтобы существовал предел . ▲

Def: Несобственный интеграл называется сходящимся абсолютно, если сходится интеграл от модуля подынтегральной функции .

Т⁰. Абсолютно сходящийся интеграл сходится.

D Пусть интеграл 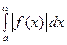сходится Þ (по критерию Коши)

, но и,

следовательно, . ▲

Т⁰. Для интегралов от неотрицательных функций сходимость эквивалентна ограниченности в совокупности интегралов по всем замкнутым промежуткам и, при этом, если

Þ .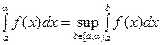

D Пусть Þ . Кроме того, функция не убывает:

. Поэтому . ▲

Т⁰. Замена переменной со строго монотонной функцией. Если строго монотонная функция, то замена сохраняет абсолютную сходимость интеграла.

D. Если функция не убывающая, то и, следовательно,

.

Крайние члены этой цепочки одновременно сходятся или расходятся. ▲

Замечание: Интегрирование по частям в общем случае не сохраняет абсолютную сходимость.

Пример: Рассмотрим 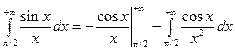. При этом, интеграл справа сходится абсолютно, а интеграл слева не сходится абсолютно. Мы это установим несколько позже.

Дата добавления: 2014-01-11