Элементы теории поверхностей

1⁰. Пусть в области G 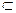Е₃ задана функция F (x, y, z) = 0 и .

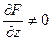Тогда выполняются условия теоремы о неявных функциях и говорят, что в области

G неявно задана поверхность z = z (x, y).

2⁰. Если нам удается разрешить уравнение F (x, y, z) = 0 относительно z, то

получаем поверхность, заданную явно: z = z (x, y).

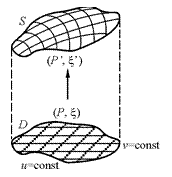3⁰. Есл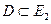и и 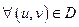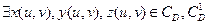, то говорят, что в 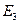задана гладкая поверхность S, а 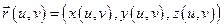– называют носителем этой поверхности.

При этом, есл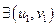и и 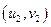такие, что

,

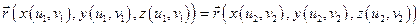то поверхность называется поверхностью с самопересечениями, в противном случае – поверхность называется простой.

Проведя в области D координатные линии 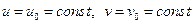мы, тем самым, индуцируем на поверхности S лини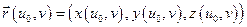и: и 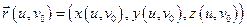, которые называются координатными линиями поверхности.

Векторы: 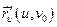и 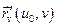являются векторами, касательными к координатным

линиям. Из соображений простоты штрих в дальнейшем не будем писать т.е. будем писать:

, .

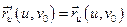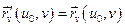Рассмотрев в точке 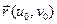векторы 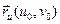и 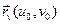, можно найти вектор 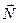перпендикулярный поверхности:

,

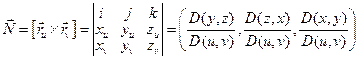Если ввести обозначения 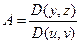, , , 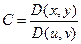то единичный вектор нормали можно записать так:

.

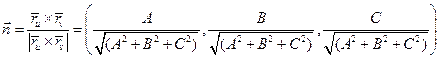Можно построить и еще один вектор нормали .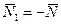

Величины являются направляющими косинусами нормали и поверхности.

В точке (x ₀, y ₀, z ₀): 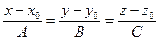– уравнение прямой, перпендикулярной к поверхности, а – уравнение плоскости касательной к поверхности.

Def. Если на поверхности S существует непрерывный замкнутый контур γ

такой, что при движении по этому контуру (с непрерывным изменением нормали) мы возвращаемся в исходную точку с нормалью имеющей противоположное исходному направлению, то поверхность называется односторонней.

Пример: Лист Мебиуса.

Def. Если для того, чтобы вернуться в исходную точку с направлением

нормали, противоположным исходному, необходимо пересечь край

поверхности, то поверхность называется двухсторонней.

*). Краем поверхности называется образ границы D в представлении .

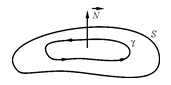
Выбрав на двусторонней поверхности контур γ, зададим на нем ориентацию, указав направление его обхода.

Теперь сориентируем поверхность выбрав на ней направление нормали так, чтобы, если смотреть с конца вектора , движение по контуру γ было против часовой стрелки. Ясно, что такая договоренность означает, что ориентация контура автоматически задает ориентацию (сторону) поверхности и наоборот.

Дата добавления: 2014-01-11