Скалярные поля

0

Пусть в Е ₃ задана поверхность : ;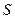

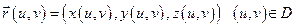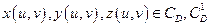, и на поверхности S задана вектор-функция

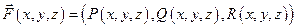
и, при этом .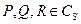

Рассмотрим:.

Если такой предел существует и конечен, то он называется поверхностным интегралом 2-го рода и обозначается .

Физический смысл поверхностного интеграла 2-го рода – поток векторного поля 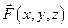через поверхность S в направлении нормали, определяемой вектором 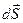, т.е. стороной поверхности. Собственно говоря, это и есть определение потока векторного поля через поверхность.

Свойства поверхностного интеграла 2-го рода:

1°. Интеграл меняет знак при изменении стороны поверхности, по которой идет интегрирование: .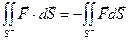

2°. Связь с поверхностным интегралом 1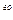рода.

.

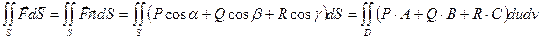Здесь единичный вектор нормали к поверхности; – направляющие косинусы нормали к поверхности; ,,;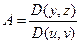

.

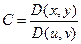3°. Если помнить о том, что: ,

, , легко написать формулу для вычисления поверхностного интеграла 2-го рода

.

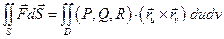Примеры вычисления поверхностных интегралов 2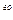рода.

1°. Вычислить , где S – внешняя сторона сферы =

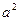
Вектор нормали 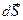был найден в предыдущем параграфе, в примере 3°.

.

Знак в выражении для 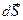берем так, чтобы в 1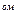октанте координаты вектора 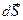были положительными (внешняя сторона).

.

Вектор .

Тогда: =

= . ▲

2°. Вычислить 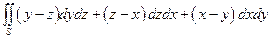, если S - внешняя сторона конуса

с крышкой z = 1.

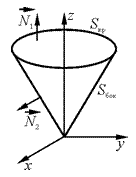Δ Поверхность интегрирования состоит из двух частей – боковой поверхности конуса и крышки. Поэтому: .

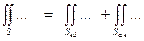а). Для вычисления первого из них, отметим что и, следовательно:

.

б). Для вычисления второго из них, вспомним что для поверхности, заданной явно:. Знак выбран так, чтобы получить внешнюю нормаль к поверхности. Получаем:

.

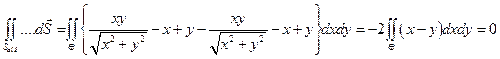Таким образом .

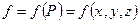Пусть задана область в евклидовом пространстве и в задана функция . Тогда говорят, что в задано скалярное поле (синоним: функция трех переменных). Поверхности 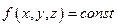называются поверхностями уровня скалярного поля.

Пусть задан вектор с известными направляющими косинусами .

Производной скалярного поля по направлению называется величина:

.

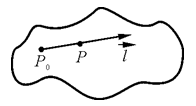
Запишем параметрическое уравнение прямой :

;

Тогда на этой прямой:

и тогда:

.

Вводя вектор 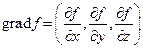получим: .

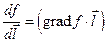Из делаем вывод, что вектор 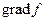указывает направление максимального роста поля и по величине равен скорости роста поля в этом направлении.

Такое определение 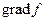является инвариантным относительно системы координат.

Если для векторного поля 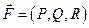существует скалярное поле 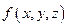такое, что то поле 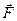называется потенциальным полем а скалярное поле 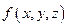называется его потенциалом.

Необходимое и достаточное условие потенциальности поля :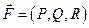

.

Дата добавления: 2014-01-11