
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поверхностные интегралы 1-го рода
|
|
|
|
Пусть в Е 3 задана поверхность 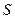 :
: 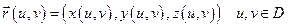 ;
;
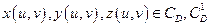 , и на поверхности S задана функция
, и на поверхности S задана функция 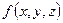 .
.
Проводя в области 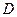 координатные линии
координатные линии  и
и  , получим в области
, получим в области 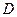 разбиение
разбиение 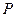 . В каждом элементе разбиения отметим точку
. В каждом элементе разбиения отметим точку 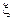 .
.
Разбиение 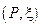 с отмеченными точками индуцирует на
с отмеченными точками индуцирует на 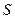 также разбиение с отмеченными точками
также разбиение с отмеченными точками 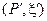 . В каждый отмеченной точке построим касательную плоскость к поверхности. Заменим поверхность
. В каждый отмеченной точке построим касательную плоскость к поверхности. Заменим поверхность 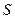 на чешуйчатую поверхность, состоящую из кусочков касательных плоскостей.
на чешуйчатую поверхность, состоящую из кусочков касательных плоскостей.
Рассмотрим: 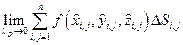 . Здесь
. Здесь 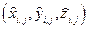 – координаты отмеченной точки,
– координаты отмеченной точки,  – скалярный элемент площади. Если такой предел существует, то он называется поверхностным интегралом 1-го рода и обозначается
– скалярный элемент площади. Если такой предел существует, то он называется поверхностным интегралом 1-го рода и обозначается  .
.
 .
.
Физический смысл поверхностного интеграла 1-го рода – масса поверхности S с поверхностной плотностью  .
.
Свойства:
1°. Условие нормировки:  . Это условие обозначает, что поверхностный интеграл 1-го рода от единицы численно равен площади поверхности.
. Это условие обозначает, что поверхностный интеграл 1-го рода от единицы численно равен площади поверхности.
2°. Интеграл не зависит от стороны двухсторонней поверхности, по которой
идет интегрирование: 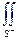

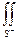
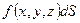 .
.
3°. О нахождении  :
: 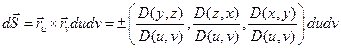 Þ
Þ
Þ  =
= 
 .
.
Еще рассмотрим: 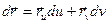 .
.
 =
=  =
=  ,
,
Здесь: 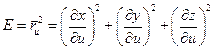 ,
,  ,
,
 .
.
Величина:  называется первой квадратичной формой поверхности. Эта квадратичная форма положительно определена. Ее матрица:
называется первой квадратичной формой поверхности. Эта квадратичная форма положительно определена. Ее матрица: 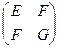 и, следовательно, по критерию Сильвестра:
и, следовательно, по критерию Сильвестра: 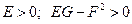 .
.
Теперь отметим, что: 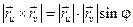 и
и 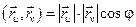 . Возведем оба соотношения в квадрат и сложим. Получим:
. Возведем оба соотношения в квадрат и сложим. Получим: 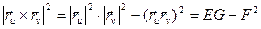 .
.
Тогда:  .
.
4°. 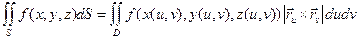 .
.
 .
.
Примеры вычисления поверхностных интегралов  рода:
рода:
1°. Вычислить  , где
, где 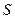 – часть поверхности параболоида
– часть поверхности параболоида  , отсекаемая плоскостью
, отсекаемая плоскостью  .
.
 Δ. Запишем параметрическое уравнение заданной поверхности:
Δ. Запишем параметрическое уравнение заданной поверхности:
 .
.
Находя вектор нормали к поверхности 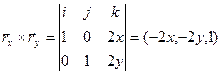 , можем найти и элемент поверхности
, можем найти и элемент поверхности 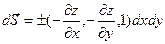 Þ
Þ  .
.
Параллельно получена формулы нахождения 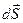 и
и  для для функции заданной явно:
для для функции заданной явно:
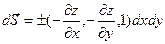 ,
,  .
.
Тогда, вычисляя исходный интеграл, получаем:
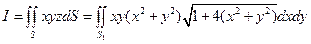 . Здесь
. Здесь  – проекция поверхности интегрирования на плоскость
– проекция поверхности интегрирования на плоскость  , т.е. круг единичного радиуса. Переходя в полярную систему координат, вычисляем интеграл:
, т.е. круг единичного радиуса. Переходя в полярную систему координат, вычисляем интеграл:
 . ▲
. ▲
 2°. Вычислить
2°. Вычислить  , если S - граница тела:
, если S - граница тела: 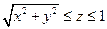 .
.
Δ. Поверхность интегрирования состоит из двух частей – боковой поверхности конуса и крышки. Поэтому 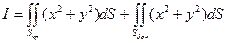 .
.
Первый из этих интегралов – интеграл по кругу единичного радиуса и
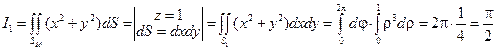 .
.
Для вычисления второго из интегралов запишем параметрическое уравнение конуса в виде:  и векторный и скалярный элементы площади поверхности:
и векторный и скалярный элементы площади поверхности: 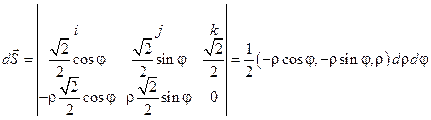 и
и  . Тогда для искомого интеграла получаем:
. Тогда для искомого интеграла получаем:
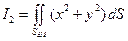 =
=  .▲
.▲
И, наконец,  .
.
3°. Вычислить  , если S – полусфера
, если S – полусфера 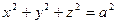 ,
,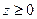 .
.
 Δ. Параметрическое уравнение сферы радиуса а:
Δ. Параметрическое уравнение сферы радиуса а:
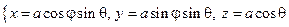 .
.
Тогда  =
=
= 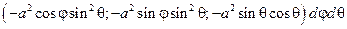 Þ
Þ
Þ 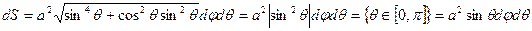 .
.
Тогда:  =
=
= 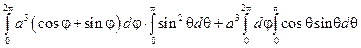 = 0.
= 0.
 §. Поверхностные интегралы 2
§. Поверхностные интегралы 2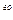 рода.
рода.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1900; Нарушение авторских прав?; Мы поможем в написании вашей работы!