Арифметические действия с пределами

Теорема 4.4.10. Пусть функции f (x), g (x) имеют предел при х ® a, С=const. Тогда имеют пределы функции С f (x), f (x)± g (x), f (x) g (x), (если ), и

4.4.10.1. ;

4.4.10.2. ;

4.4.10.3. ;

4.4.10.4. .

Док-во основано на теор. 4.4.9 о связи функции с её пределом. Пусть 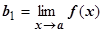, Þ f (x)= b ₁+a(х), g (x)= b ₂+b(х), где a(х), b(х) - БМ. Тогда:

4.4.10.1. С f (x)=С b ₁+Сa(х); Сa(х) - БМ по теор. 4.4.7 Þ$.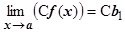

4.4.10.2. 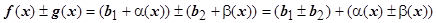; a(х)±b(х) - БМÞ

$.

4.4.10.3. . Выражение в квадратных скобках - БМ (теор. 4.4.3, 4.4.7, 4.4.8) Þ$.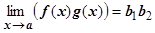

4.4.10.4. Оценим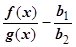: . В числителе стоит БМ, функция 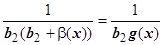- ограничена при (почему?) Þ$.

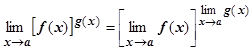С двумя функциями можно произвести ещё следующие действия: возвести f (x) в степень g (x) и взять их суперпозицию. Для степени f (x) ^{g ( x )} оказывается, что если существуют конечные , , то существует , это следствие непрерывности показательной и логарифмической функций; и этот вопрос будет рассмотрен ниже. Для суперпозиции функций оказывается, что существование пределов внешней и внутренней функций недостаточно для существования предела сложной функции. Более точно, если х = g (t) имеет предел а при t ® t₀, функция y = f (x) имеет предел при x ® а, то 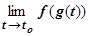может не существовать. Пример: пусть . Очевидно, $. Пусть . $. 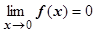Для последовательности точек ; если выбрать последовательность , не попадающую в эти точки, то 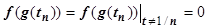. Две последовательности дают разные пределыÞне существует. Дальше мы увидим, что существование предела сложной функции обеспечивает непрерывность внешней функции.

4.4.7. Замечательные пределы.

4.4.7.1. Первый замечательный предел. Так принято называть . Докажем, что он равен единице. 1. Докажем, что sin| x |£.| x | (достаточно доказать это при х >0). Рассмотрим круг радиуса 1 с центром в точке О. В качестве переменной х будем брать центральный угол, отсчитываемый в радианах от радиуса ОА. Тогда длина дуги АВ = х, длина отрезка ВD =sin х, sin х < х (при х ¹0; перпендикуляр - кратчайшее расстояние от точки до прямой). 2. Сравним площади треугольников OBА, OCA и сектора OBA: S(тр. OBА)<S(сек. OBA)<S(тр. OCA). Выразим эти площади: (CA =tg x). Делим это выражение на 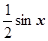: . Мы получили эти неравенства в предположении х >0, но вследствие четности входящих в них выражений они верны при любом знаке х. 3. Переворачиваем эти неравенства: 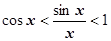. cos x ®1 при х ®0, предел правой части тоже равен 1, по теор. 3.4.5 о пределе промежуточной функции $.

Следствия: .

4.4.7.2. Второй замечательный предел. Изучая пределы последовательностей, мы доказали, что $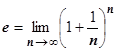. Распространим это доказательство на случай действительной переменной, докажем, что . Пусть n = E (x), тогда n £ x < n +1. Если x ®+¥, то и n ®¥, поэтому можем считать n >1. Из неравенства 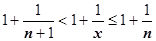вследствие монотонного возрастания степенной функции с аргументом и степенью >1, получим . Предел правого члена при n ®¥ равен числу е, предел левого тоже равен числу е. По теор. 4.4.6 о пределе промежуточной функции $, и он тоже равен числу е. Далее, 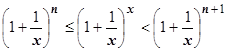, и снова применяя теор. 4.4.6 о пределе промежуточной функции, получаем, что существует и равен числу е.

Пусть теперь x ®-¥. Введём новую переменную y =- x -1,тогда x =- y -1, и y ®+¥ при x ®-¥. 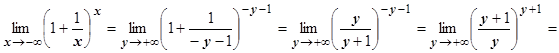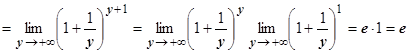. Доказано, что односторонние пределы при x ®±¥ существуют и равныÞ(по теор. 4.4.1) $.

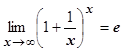4.4.7.2.1. Эквивалентная форма второго замечательного предела: 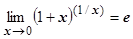(сводится к предыдущему случаю заменой ).

4.4.7.3. Следствия из замечательных пределов. Рассмотрим еще несколько важных пределов.

4.4.7.3.1. . Док-во: .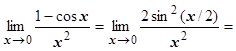

4.4.7.3.2. . Док-во: 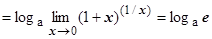. (Здесь мы пользуемся непрерывностью функции .) Следствие: 4.4.7.3.2.1. .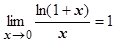

4.4.7.3.3. . Док-во: заменим переменную .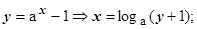

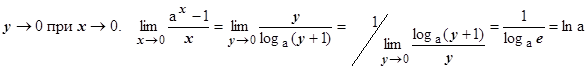Следствие: 4.4.7.3.3.1. .

4.4.7.3.4. 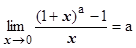. Док-во: заменим переменную .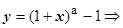

4.4.7.3.5.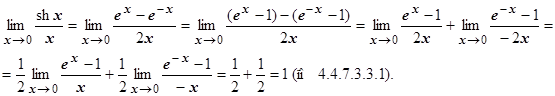

4.4.7.3.6.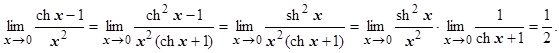

Дата добавления: 2014-01-11