
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выделение главной части функции
|
|
|
|
Выделение главной части функции - мощный приём при решении задач на вычисление пределов. Основная цель выделения главной части - получение более простой функции, которая в окрестности предельной точки ведёт себя также, как исходная громоздкая (тогда по теореме 4.4.9.2 о замене бесконечно малых на эквивалентные мы можем заменить громоздкие функции в числителе и знаменателе на эквивалентные простые); основной инструмент при выделении главных частей - табл. 4.4.10 эквивалентных бесконечно малых.
Как следует из определений разделов 4.4.8-4.4.11, утверждения "при х ® а 1. f (x)~ g (x); 2. f (x)- g (x)=o(g (x)) =o(f (x)); 3. g (x) есть главная часть f (x)" эквивалентны. Так как для f (x) может существовать бесконечно много главных частей при х ® а (например, при х ®0 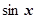 ~
~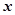 ~
~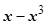 ~ ~
~ ~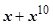 ~
~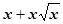 ~ …..), при выделении главных частей указывается их вид; при решении задач на вычисление пределов при х ® а обычно это С0(х - а)k для бесконечно малых и
~ …..), при выделении главных частей указывается их вид; при решении задач на вычисление пределов при х ® а обычно это С0(х - а)k для бесконечно малых и 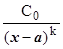 для бесконечно больших, при х ®¥ - это
для бесконечно больших, при х ®¥ - это 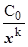 для бесконечно малых и
для бесконечно малых и 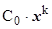 для бесконечно больших, где С0 = const¹0, k =const>0 – порядок малости или роста функции f (x) относительно функции (х - а) (или относительно
для бесконечно больших, где С0 = const¹0, k =const>0 – порядок малости или роста функции f (x) относительно функции (х - а) (или относительно 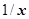 при х ®¥). Для главных частей такого вида бесконечно малых при х ® а функций равносильны следующие утверждения:
при х ®¥). Для главных частей такого вида бесконечно малых при х ® а функций равносильны следующие утверждения:
1. 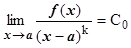 ;
;
2. 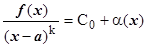 , где a(х) – БМ при х ® а;
, где a(х) – БМ при х ® а;
3. 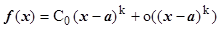 ;
;
4. 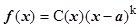 , где
, где 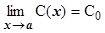 ;
;
5. f (x) ~ 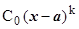 .
.
Таким образом, в простейших случаях рецепт для выделения главной части вида С0(х - а)k БМ при х ® а функции f (x) состоит в следующем: f (x) надо представить в виде f (x)=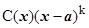 , где
, где 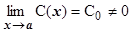 . Тогда
. Тогда 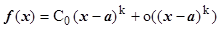 , и
, и 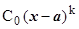 - главная часть функции f (x) при х ® а.
- главная часть функции f (x) при х ® а.
Аналогично изложенному выше, с заменой (х - а)k на 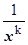 , формулируются утверждения и правило для выделения главной части функции, бесконечно малой при х ®¥.
, формулируются утверждения и правило для выделения главной части функции, бесконечно малой при х ®¥.
Рассмотрим ряд примеров на выделение главной части и определение порядка малости функций (в скобках указываются применённые формулы табл. 4.4.10):
1. 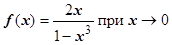 . Представим f (x) в виде
. Представим f (x) в виде 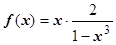 . Если
. Если 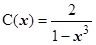 , то
, то 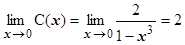 , поэтому
, поэтому 
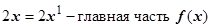 , k=1 – порядок малости f (x) при х ®0.
, k=1 – порядок малости f (x) при х ®0.
2.  . Представим f (x) в виде
. Представим f (x) в виде 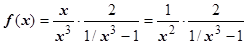 . Если
. Если 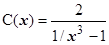 , то
, то 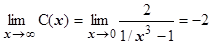 , поэтому
, поэтому 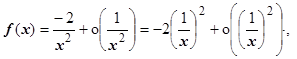
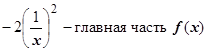 , k=2 – порядок малости f (x) при х ®¥ по сравнению с
, k=2 – порядок малости f (x) при х ®¥ по сравнению с 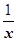 .
.
3. 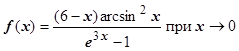 . С помощью формул 4,6 таблицы 4.4.10 представим f (x) в виде
. С помощью формул 4,6 таблицы 4.4.10 представим f (x) в виде 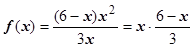 . Здесь
. Здесь  ,
, 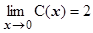 , поэтому
, поэтому 
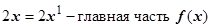 , k=1 – порядок малости f (x) при х ®0.
, k=1 – порядок малости f (x) при х ®0.
4. 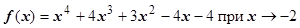 . Так как f (-2) = 0, то
. Так как f (-2) = 0, то 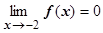 , и многочлен
, и многочлен 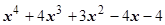 делится на х + 2 без остатка. Произведя деление, получим
делится на х + 2 без остатка. Произведя деление, получим 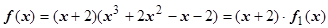 . Так как и f 1(-2) = 0, то
. Так как и f 1(-2) = 0, то 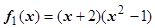 , поэтому
, поэтому 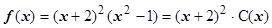 , где
, где 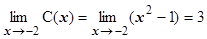 . Результат:
. Результат:  ,
, 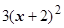 - главная часть f (x), k=2 – порядок малости f (x) при х ®-2.
- главная часть f (x), k=2 – порядок малости f (x) при х ®-2.
5. 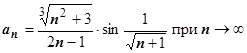 .
. 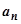 ~
~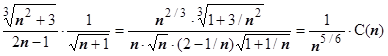 , где
, где 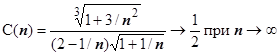 . Поэтому
. Поэтому 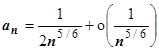 ,
, 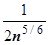 - главная часть
- главная часть 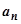 , k=5/6 (относительно БМ
, k=5/6 (относительно БМ 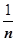 ) при
) при 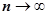 .
.
В следующих задачах решение излагается более кратко.
6. 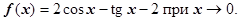
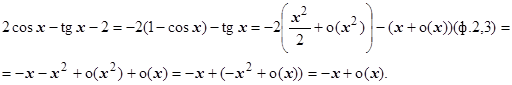
7. 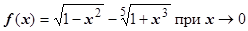 .
.
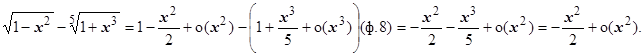
8. 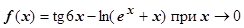 .
.
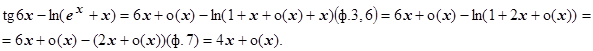
9. 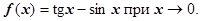
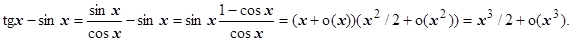
Неаккуратность при решении последнего примера даст результат
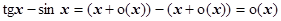 верный, но бесполезный.
верный, но бесполезный.
10. Пусть х ®+0. Тогда
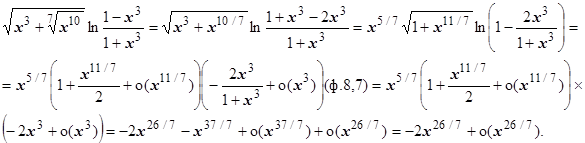
Если рассматривается случай х ® а ¹ 0, часто полезно сделать замену переменной у = х - а.
Пример:
11. Пусть х ®2. Найти главную часть БМ функции 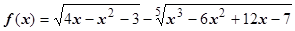 (убедитесь, что f (x) ®0 при х ®2). Перейдём к переменной у = х -2Þ х = у +2; у ®0 при х ®2. Меняем в функции х на у +2:
(убедитесь, что f (x) ®0 при х ®2). Перейдём к переменной у = х -2Þ х = у +2; у ®0 при х ®2. Меняем в функции х на у +2:
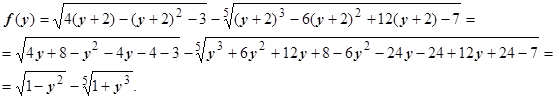
Так как у ®0, мы пришли к задаче, рассмотренной в примере 2. Ответ: 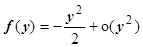 ,
, 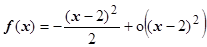 при х ®2.
при х ®2.
12. Для функции, представляющей собой линейную комбинацию степенных выражений 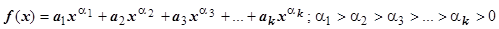 легко показать, что при х ®0 f (x) эквивалентна своему слагаемому с минимальной степенью: f (x)~
легко показать, что при х ®0 f (x) эквивалентна своему слагаемому с минимальной степенью: f (x)~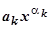 :
: 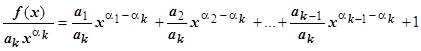 и все слагаемые, кроме последнего, стремятся к нулю при х ®0, так как
и все слагаемые, кроме последнего, стремятся к нулю при х ®0, так как 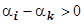 при i =1,2,…, k -1.
при i =1,2,…, k -1.
При х ®¥ f (x) эквивалентна своему слагаемому с максимальной степенью f (x)~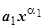 :
:  и все слагаемые, кроме первого, стремятся к нулю при х ®¥, так как
и все слагаемые, кроме первого, стремятся к нулю при х ®¥, так как 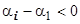 при i =2,…, k.
при i =2,…, k.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 11850; Нарушение авторских прав?; Мы поможем в написании вашей работы!