
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Гаусса. Метод Гаусса основан на приведении матрицы системы к треугольному виду
|
|
|
|
Метод Гаусса основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы.
Сначала с помощью первого уравнения исключается 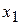 из второго и всех последующих уравнений системы. Затем с помощью второго уравнения исключается
из второго и всех последующих уравнений системы. Затем с помощью второго уравнения исключается 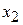 из третьего и всех последующих уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего (n -го) уравнения не останется лишь один член с неизвестным
из третьего и всех последующих уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего (n -го) уравнения не останется лишь один член с неизвестным 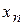 , т. е. матрица системы будет приведена к треугольному виду. Этот процесс называется прямым ходом метода Гаусса.
, т. е. матрица системы будет приведена к треугольному виду. Этот процесс называется прямым ходом метода Гаусса.
Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим 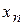 ; далее, используя это значение, из предпоследнего уравнения вычисляем
; далее, используя это значение, из предпоследнего уравнения вычисляем 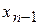 и т.д. Последним будет найден
и т.д. Последним будет найден 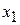 из первого уравнения.
из первого уравнения.
Проиллюстрируем метод Гаусса на примере решения системы из трех линейных уравнений; в этом случае (то есть для n = 3) система (2.1) запишется в следующем виде:
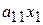
| + | 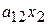
| + | 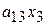
| = | 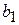 , ,
| (4.6) |
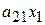
| + | 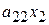
| + | 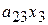
| = | 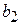 , ,
| (4.7) |
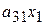
| + | 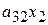
| + | 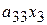
| = |  . .
| (4.8) |
Предполагается, что 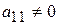 . Если это не так, необходимо переставить уравнения (4.6) – (4.8) таким образом, чтобы в первом уравнении коэффициент при
. Если это не так, необходимо переставить уравнения (4.6) – (4.8) таким образом, чтобы в первом уравнении коэффициент при 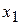 не был равен нулю.
не был равен нулю.
Решение будем выполнять поэтапно, обозначая каждый этап через k 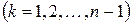 .
.
k = 1
i = 2. Определим множитель 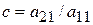 для уравнения (2.7).
для уравнения (2.7).
Умножим первое уравнение, т.е. (4.6), на множитель 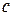 и вычтем из второго:
и вычтем из второго:
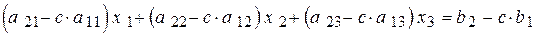 . (4.9)
. (4.9)
Используя обозначения 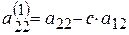 ,
, 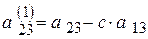 и
и 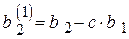 и учитывая, что в уравнении (4.7) коэффициент при
и учитывая, что в уравнении (4.7) коэффициент при 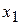 равен нулю (так как, подставляя выражение для c, получаем
равен нулю (так как, подставляя выражение для c, получаем 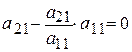 ) уравнение (4.7) запишется в следующем виде:
) уравнение (4.7) запишется в следующем виде:
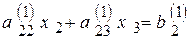 .
.
i = 3. Определим множитель 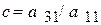 и выполним ту же самую процедуру для третьего уравнения (4.8) c использованием соответствующих обозначений, тогда искомая система (4.6) – (4.8) примет следующий вид:
и выполним ту же самую процедуру для третьего уравнения (4.8) c использованием соответствующих обозначений, тогда искомая система (4.6) – (4.8) примет следующий вид:
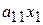
| + | 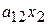
| + | 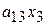
| = | 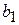 , ,
| (2.2, а) |
| + | 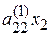
| + | 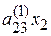
| = | 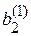 , ,
| (2.3, а) | |
| + | 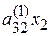
| + | 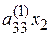
| = | 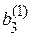 . .
| (2.4, а) |
Как видим, остается преобразовать последнее уравнение в системе (2.2, а) – (2.4, б) для приведения системы к треугольному виду; поэтому переходим к следующему этапу.
k = 2
i = 3. По схеме, аналогичной для случая k = 2, вводим множитель 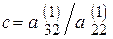 , умножаем второе уравнение (2.2, а) на множитель
, умножаем второе уравнение (2.2, а) на множитель 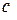 и вычитаем из третьего и, используя соответствующие обозначения и учитывая, что коэффициент при
и вычитаем из третьего и, используя соответствующие обозначения и учитывая, что коэффициент при 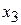 в третьем уравнении равен нулю (ср. с (2.2, а) и (2.3,а)), получаем окончательно треугольную матрицу для нашей системы:
в третьем уравнении равен нулю (ср. с (2.2, а) и (2.3,а)), получаем окончательно треугольную матрицу для нашей системы:
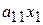
| + | 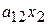
| + | 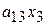
| = | 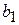 , ,
| (4.10) |
| + | 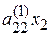
| + | 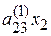
| = | 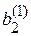 , ,
| (4.11) | |
| + | + | 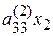
| = | 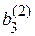 . .
| (4.12) |
где 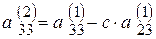 ,
, 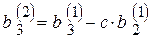 .
.
Для системы (4.10) – (4.12), выполняют обратный ход, т.е находят сначала 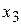 из уравнения (4.12) и затем, подставляя его в (4.11), находят
из уравнения (4.12) и затем, подставляя его в (4.11), находят 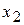 ; аналогично определяют
; аналогично определяют 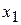 :
:
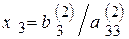 , (4.13)
, (4.13)
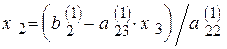 , (4.14)
, (4.14)
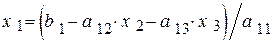 =
= 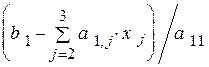 . (4.15)
. (4.15)
Схему решения для любого значения n будет следующая:
Прямой ход:
На этапе k неизвестная  исключается введением множителя
исключается введением множителя
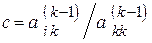 ,
, 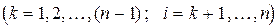 (4.16)
(4.16)
и выполнением следующих вычислений:
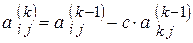 , (4.17)
, (4.17)
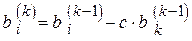 . (4.18)
. (4.18)
Обратный ход.
Сначала вычисляется значение неизвестной 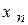 :
:
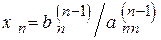 ; (4.19)
; (4.19)
а затем последовательно вычисляются остальные неизвестные 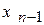 ,
, 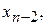 …,
…, 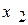 ,
, 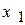 :
:
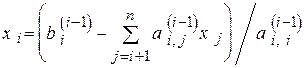 , (4.20)
, (4.20)
здесь 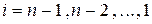 .
.
Заметим, в формулах не записывались верхние нулевые индексы (0).
4.3 Метод прогонки
Пусть имеется разреженная система с трехдиагональной матрицей, т.е. ненулевые элементы находятся лишь на главной и двух соседней с ней диагоналях, расположенных сверху и снизу (см.(4.5)):
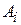
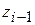 +
+ 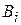
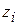 +
+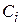
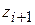 =
= 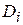 , (4.21)
, (4.21)
i = 1, 2, …, n; 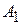 = 0,
= 0, 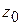 =0,
=0, 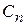 = 0,
= 0, 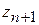 =0,
=0, 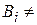 0, (4.22)
0, (4.22)
тогда данная система,, например из пяти уравненй (n = 5), запишется так:
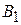 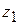 + +
| 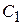 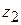
| =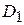 , ,
| |||
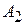 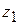 + +
| 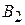 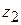 + +
| 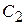 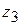
| =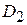 , ,
| ||
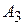 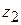 + +
| 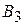 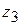 + +
| 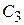 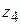
| =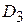 , (4.23) , (4.23)
| ||
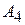 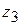 + +
| 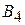 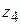 + +
| 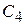 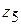
| =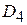 , ,
| ||
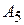 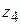 + +
| 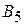 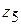
| =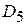 . .
|
Замечание. В дальнейшем, при выводе рабочих формул, ссылку будем делать в основном на систему (4.23), предполагая, что последнее (пятое) уравнение имеет порядковый номер п.
Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений. Для решения системы (4.21) – (4.22) обычно применяется метод прогонки, который является частным случаем метода Гаусса, и состоит из двух этапов – прямой прогонки (аналог прямого хода) и обратной прогонки (аналог обратного хода метода Гаусса).
Прямая прогонка состоит в том, что каждое неизвестное 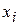 выражается через
выражается через 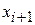 с помощью прогоночных коэффициентов
с помощью прогоночных коэффициентов 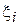 и
и 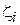 :
:
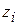 =
= 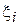
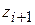 +
+ 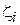 , i = 1, 2, …, n – 1. (4.24)
, i = 1, 2, …, n – 1. (4.24)
Коэффициенты 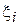 и
и 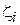 вычисляются следующим образом.
вычисляются следующим образом.
Первое уравнение системы (4.23) разрешим относительно 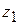 , а уравнение (4.21) запишем для i = 1:
, а уравнение (4.21) запишем для i = 1:
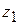 =(–
=(–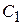 /
/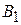 )
)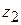 + (
+ (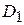 /
/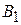 ),
),
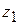 =
= 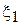
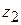 +
+ 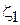 . (4.25)
. (4.25)
Приравнивая коэффициенты при неизвестных 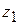 и
и 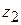 , получаем:
, получаем:
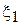 = –
= –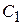 /
/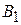 ,
, 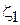 =
= 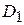 /
/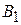 . (4.26)
. (4.26)
Второе уравнение системы (4.23) запишем, заменяя 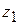 по формуле (4.25):
по формуле (4.25):
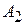 (
(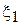
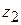 +
+ 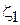 ) +
) + 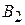
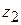 +
+ 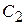
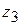 =
= 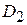 .
.
Отсюда находим:
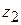 = [–
= [–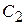 /(
/(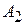
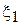 +
+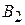 )]
)]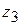 + (
+ (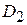 –
–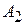
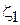 )/(
)/(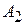
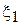 +
+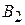 )
)
Но, с другой стороны (см. (4.24)),
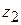 =
= 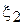
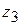 +
+ 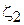 .
.
Сравнивая последнее уравнение с предшествующим, определяем:
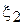 = –
= –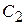 /(
/(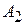
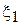 +
+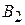 ),
), 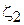 = (
= (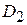 –
–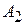
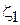 )/(
)/(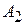
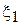 +
+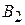 ).
).
То есть, формулы для вычисления 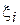 и
и 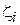 (i = 2, 3,…, n – 1) будут следующие:
(i = 2, 3,…, n – 1) будут следующие:
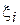 =
= 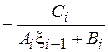 ,
, 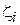 =
= 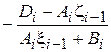 , (4.27)
, (4.27)
Таким образом, в результате выполнения первого этапа (проведения прямой прогонки), последовательно применяя формулы (4.26) и (4.27), вычисляем все значения 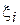 и
и 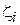 (i = 1, 2, …, n – 1).
(i = 1, 2, …, n – 1).
Обратная прогонка заключается в последовательном вычислении неизвестных 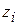 . С этой целью сначала нужно найти
. С этой целью сначала нужно найти 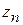 . Если воспользоваться выражениями (4.24) при i = n – 1 и последним уравнением системы (4.23) (учитывая замечание к этой системе), получим:
. Если воспользоваться выражениями (4.24) при i = n – 1 и последним уравнением системы (4.23) (учитывая замечание к этой системе), получим:
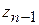 =
= 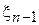
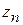 +
+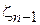 ,
,
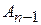
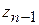 +
+ 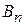
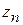 =
= 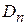 .
.
Исключая 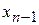 из последних двух выражений, находим
из последних двух выражений, находим
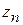 =
= 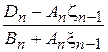 . (4.28)
. (4.28)
Далее, используя вычисленные значения 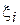 и
и 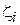 , по формуле (4.24) последовательно вычисляем
, по формуле (4.24) последовательно вычисляем 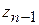 ,
, 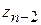 , …,
, …, 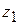 .
.
Метод прогонки из-за его устойчивости можно применять для решения больших систем уравнений.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1149; Нарушение авторских прав?; Мы поможем в написании вашей работы!