Системы исчисления. Правила перевода из одной системы исчисления в другую

Математические основы цифровой схемотехники

Системой исчисления называют систему приемов и правил, которые позво­ляют устанавливать взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. В зависимости от способа изображения чисел с помощью цифр системы исчисления делятся на позиционные и непозиционные.

В непозиционных системах любое число определяется как некоторая функ­ция от численных значений совокупности цифр, которые представляют это
число. Цифры в непозиционных системах исчисления отвечают некоторым
фиксированным числам. Позиционной система исчисления называется
потому, что значение каждой входящей в число цифры зависит, от ее поло­-
жения в записи числа.

Любая позиционная система исчисления с основой q может быть представлена в виде полинома

,

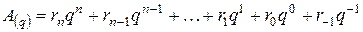где А — число в позиционной системе исчисления с основой q; — коэф­фициент; n — степень и индекс.

Позиционные системы исчисления бывают разными в зависимости от осно­вы: десятичные с основой десять, восьмеричные с основой восемь, двоичные с основой два и т. д.

В двоичной системе исчисления коэффициентами , являются цифры 0 и 1, а основой — число 2. В общем виде число в двоичной системе исчисления бу­дет записано как:

.

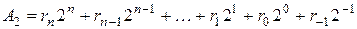Цифровые устройства используют элементы, которые имеют только два устойчивых состояния, поэтому двоичная система исчисления приобрела широчайшее распространение для представления и обработки информации.

Восьмеричная система применяется для выполнения вспомогательных функ­ций, сокращает запись числовой информации и обеспечивает простоту пере­вода в двоичную систему, поскольку любая восьмеричная цифра легко заме­няется двоичным трехразрядным числом — триадой. Наиболее удобной и короткой по записи является шестнадцатеричная позиционная система. Ос­новой системы служит число 16, а как коэффициенты приняты цифровые и буквенные символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.

Перевод из десятичной системы в любую позиционную систему исчисления проводится методом последовательного деления на основу новой системы до тех пор, пока остаток от деления не будет меньше основы системы. Число в новой системе записывается в виде остатков от деления, начиная с послед­него остатка, справа налево. Дробное число записывается в виде целых час­тей чисел, которые получают при умножении только дробной части на осно­ву, начиная сверху после запятой, и при этом задается точность вычислений.

Во многих практических приложениях, например, при аналогово-цифровом преобразовании данных, желательно пользоваться кодами, в кото­рых все последовательные кодовые наборы отличаются один от другого только одним разрядом. Такие коды называются циклическими кодами. Особенно важным среди циклических кодов является код Грэя, который при­веден в таблице 1.

Код Грэя используется в механических шифраторах угла поворота вала, при "параллельном кодировании" — методе быстродействующего аналогово-циф-рового преобразования. Это позволяет предотвратить ошибки, поскольку в этом случае при переходе между двумя закодированными значениями все разряды никак не могут измениться одновременно. Если бы использовался чисто двоичный код, то при переходе, например, от 7 до 8, на выходе можно было бы получить число 15.

Существует ряд других кодов, которые обладают интересными и полезными свойствами, например, код "с остатком 3" или код "4221". Для того чтобы любую цифру от 0 до 9 записать в коде с остатком 3, надо приба­вить к ней число 3, а потом выразить результат в 4-разрядном двоичном коде. При использовании кода "4221" каждая цифра также записывается в виде 4-разрядной группы. Однако ее разряды, начиная с левого, представляют ве­личины 4, 2, 2 и 1. Эти коды обладают одним весьма важным свойством: для того, чтобы для какой-нибудь цифры получить его дополнение к 9, достаточно взять ее об­ратный код. Это позволяет упростить десятеричную арифметику. Вместо вычитания какого-либо числа достаточно провести сложение с числом, кото­рое представляет собой дополнение к 9 начального числа плюс 1.

Таблица 1 - Код Грэя

Десятичное число	Двоичный код	Код Грэя

Дата добавления: 2014-01-11