
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные законы алгебры логики
|
|
|
|
Элементы математической логики
Цифровых устройств
Алгебра логики и теоретические основы синтеза
Математическая логика является частью формальной логики и служит теоретической основой построения электронных вычислительных машин и цифровых устройств. Наиболее широкое применение из области математической логики получила алгебра логики.
Базой алгебры логики являются понятия о высказывании, истинности и ложности высказывания, связях между высказываниями. Высказывание или логический аргумент в зависимости от значения бывают истинными или ложными. Значение высказывания может изменяться с изменением обстоятельств, и таким образом высказывание меняет оценку своей истинности. С точки зрения логики, высказывания можно разделить на:
□ высказывание истинно постоянно (математически их принимают равными 1); □ высказывание ложно постоянно (математически их принимают равными 0);
□ высказывание, которое может быть истинным или ложным в зависимости от определенных условий, т. е. принимать значение 1 или 0 попеременно.
По смыслу высказывания бывают простые и сложные. Простое высказывание — логический аргумент (переменная) — входит в состав сложного высказывания логической функции, которая зависит от истинности или ложности аргумента. Обычно простое высказывание обозначается малыми буквами латинского или русского алфавита: х, е, z, т, р, а, b. Сложные высказывания или логические функции, обозначают большими буквами латинского или русского алфавита: А, F, Р, X, Y, S, Q). Связи между высказываниями-аргументами по своей логике разные, и из-за этого значение сложного высказывания непостоянное.
В алгебре логики введена следующая система аксиом, которая определяет свойства и отношения основных операций:
а+b=b+а
а(b + с) = аb + ас
а + bс = (а + b)(а + с)
а +  =1
=1
а+ =b+
=b+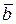
а = b
= b
На основе этих аксиом выводятся все теоремы, которые выражают основные законы алгебры логики. Их еще называют системой равносильных преобразований функции или равнозначностями:
1. Законы нулевого множества
0 = 0
= 0
0 + а = а
0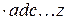 =0,
=0,
т. е. конъюнкция любого числа переменных обращается в ноль, если какая-нибудь одна переменная имеет значение 0, независимо от значений других переменных.
2. Законы универсального множества
1 = а
= а
1 + а = 1
1 + а + b +... + 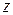 = 1,
= 1,
т. е. дизъюнкция любого числа переменных обращается в единицу, если хотя бы одна из ее переменных имеет значение 1, независимо от значений других переменных.
3. Законы идемпотентности (повторения, тавтологии)
аа...а = а
а + а +.... + а = а.
4. Законы двойной инверсии
 = а,
= а,
т. е. двойную инверсию можно снять.
5. Законы дополнительности:
а) логическое противоречие
а = 0,
= 0,
т. е. конъюнкция любой переменной и ее инверсии есть 0.
б) закон исключенного третьего а + =1,
=1,
т. е. дизъюнкция любой переменной и ее инверсии есть 1.
6. Коммутативный (закон перемещения) закон
аb = bа
a+b=b+a,
т. е. результаты выполнения операций конъюнкции и дизъюнкции не зависят от того, в каком порядке следуют переменные.
7. Ассоциативные (сочетательные) законы
а(bс) = (аb)с = аbс
а + (b+ с) = (а + b) + с = а + с + b,
т. е. для записи конъюнкции или дизъюнкции скобки можно опустить.
8. Дистрибутивные (распределительные) законы:
а) конъюнкции относительно дизъюнкции
а(b+ с) = аb + ас;
б) дизъюнкции относительно конъюнкции
а + bс = (а + b)(а + с).
9. Законы поглощения
а(а + b) = а
а(а + b)(а + с)...(а + w) = а
а + аb = а
a+аb+ ас+...+ аw = а
а( + b) = аb
+ b) = аb
а +  b = а + b.
b = а + b.
10. Законы склеивания (распространения)
аb + а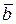 = а
= а
(а + b)(а +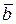 ) = а.
) = а.
11. Законы обобщенного склеивания
аb + а + bс = аb + а
+ bс = аb + а
(а + b)( + с)(b+ с) = (а + b)(
+ с)(b+ с) = (а + b)( + с)
+ с)
(а + b)( +с) = ас +
+с) = ас +  b.
b.
12. Законы де Моргана (законы инверсии):
а) для двух переменных
 =
=  +
+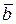 ,
,
т. е. инверсия конъюнкции есть дизъюнкция инверсий;
 =
=
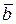 ,
,
т. е. инверсия дизъюнкции есть конъюнкция инверсий;
б) для n переменных



13. Теорема разложения
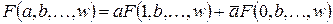

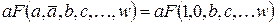
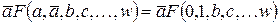

 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1052; Нарушение авторских прав?; Мы поможем в написании вашей работы!