
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 6
Для того, чтобы в т.  существовал конечный
существовал конечный 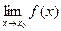 необходимо и достаточно, чтобы в этой точке существовали и были равны односторонние пределы в этой точке.
необходимо и достаточно, чтобы в этой точке существовали и были равны односторонние пределы в этой точке.
Определение 2
Функция  называется непрерывной в т.
называется непрерывной в т.  справа (resp слева) если
справа (resp слева) если 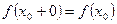 (resp
(resp 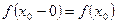 ).
).
Очевидно функция  непрерывна в т.
непрерывна в т.  тогда и только тогда, когда она непрерывна в этой точке как справа так и слева.
тогда и только тогда, когда она непрерывна в этой точке как справа так и слева.
Определение
Функция  называется непрерывной в некотором промежутке, если она непрерывна в каждой точке этого промежутка. Если один из концов промежутка находится в конечной точке
называется непрерывной в некотором промежутке, если она непрерывна в каждой точке этого промежутка. Если один из концов промежутка находится в конечной точке  и эта точка
и эта точка 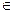 промежутку, то непрерывность функции в т.
промежутку, то непрерывность функции в т.  следует понимать в одностороннем смысле.
следует понимать в одностороннем смысле.
Например, фразу, «функция  не прерывиста на отрезке
не прерывиста на отрезке 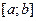 », следует понимать так, функция
», следует понимать так, функция  непрерывна в интервале
непрерывна в интервале 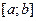 , непрерывна в точке а справа и непрерывна в точке b слева.
, непрерывна в точке а справа и непрерывна в точке b слева.




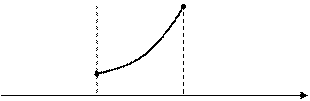
a b x
Эта функция непрерывна на отрезке 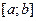
Предел функции на бесконечности.( 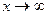 )
)
Определение 3
Последовательность 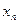 называется ББП (последовательностью) если
называется ББП (последовательностью) если 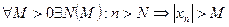 Пишут
Пишут 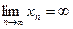 . Очевидно, ББП не ограничена. Обратное же утверждение вообще говоря неверно (пример
. Очевидно, ББП не ограничена. Обратное же утверждение вообще говоря неверно (пример 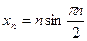 ). Если для больших n члены
). Если для больших n члены 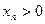 , то пишут
, то пишут 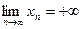 это значит, что как только
это значит, что как только 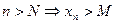 .
.
Аналогично определяется смысл записи 
Определение 4 (по Гейне)
Число А называется пределом функции  при
при 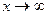 если любой ББП
если любой ББП 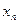 значений аргумента последовательность
значений аргумента последовательность 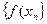 соответствующих значений функции сходится к А.
соответствующих значений функции сходится к А.
Определение 4 (по Коши).
Число А называется 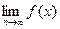 если
если 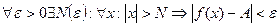 . Доказывается, что эти определения равносильны.
. Доказывается, что эти определения равносильны.
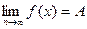
Если в определении 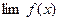 функции на бесконечности по Гейне считать в частности, что
функции на бесконечности по Гейне считать в частности, что 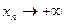 (resp
(resp 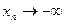 ), то тем самым определение по Гейне предел
), то тем самым определение по Гейне предел 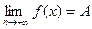 (resp
(resp 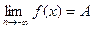 ).
).
Если же в определении 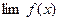 на бесконечности по Коши считать в частности, что неравенство
на бесконечности по Коши считать в частности, что неравенство  выполняется при
выполняется при 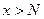 (resp
(resp 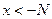 ), то тем самым определяется по Коши соответственно пределы функции
), то тем самым определяется по Коши соответственно пределы функции  на
на 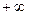 и на
и на 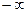 .
.
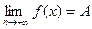 и
и 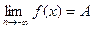
Предел последовательности есть частный случай предела функции при 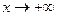 действительно возьмем последовательность {
действительно возьмем последовательность {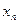 } и рассмотрим функцию
} и рассмотрим функцию  определенную на N, так что
определенную на N, так что 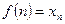 , тогда
, тогда 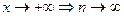 и определение предела функции при
и определение предела функции при 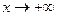 совпадает с определением предела последовательности
совпадает с определением предела последовательности 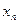 .
.
Сделаем одно общее замечание о конечном пределе функции:
Мы изучили понятие конечного предела функции  при
при 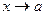 (точка а конечна или нет, т.е.
(точка а конечна или нет, т.е. 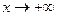 ) при этом были рассмотрены 6 возможных типов стремления аргумента х к точке а (два двусторонних и 4 односторонних), в подходе Коши каждому из этих типов отвечает свой тип окрестности А.
) при этом были рассмотрены 6 возможных типов стремления аргумента х к точке а (два двусторонних и 4 односторонних), в подходе Коши каждому из этих типов отвечает свой тип окрестности А.
| № | Тип стремления | Тип окрестности |
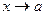 (т. а конечна) (т. а конечна)
| 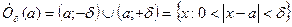
| |
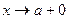 (т. а конечна) (т. а конечна)
| 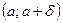
| |
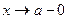 (т. а конечна) (т. а конечна)
| 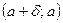
| |
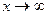
| 
| |
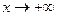
| 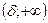
| |
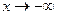
| 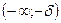
|
Условимся любой из 6 типов стремления записывать символически 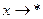 (* - любой из типов стремлений), а соответствующий ему тип окрестности
(* - любой из типов стремлений), а соответствующий ему тип окрестности 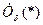 , тогда определение конечного
, тогда определение конечного 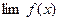 может быть дано сразу для всех шести случаев в форме:
может быть дано сразу для всех шести случаев в форме: 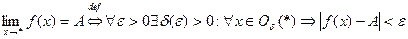 . В качестве примера использования этого общего подхода сформулируем теорему.
. В качестве примера использования этого общего подхода сформулируем теорему.
|
Дата добавления: 2014-01-11; Просмотров: 297; Нарушение авторских прав?; Мы поможем в написании вашей работы!