Теорема. Если при некотором стремлении, то ограничена в некоторой окрестности, соответствующая данному стремлению

Если 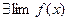при некотором стремлении, то ограничена в некоторой окрестности, соответствующая данному стремлению.

Доказательство проводится так же как в теореме 2 с очевидным изменением записи окрестности (т.е. ).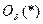

Аналогично можно построить определения конечного предела функции по Гейне при .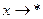

ЛЕКЦИЯ №

БМФ и их свойства.

Определение.

Функция называется БМ при 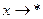, если , т.е.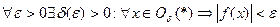

Пример:

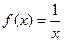- БМФ при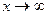

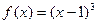- БМФ при 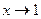(в т. х=1).

Из определения предела функции при произвольном стремлении по Коши сразу вытекает, что функция имеет конечный предел А при 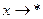тогда и только тогда, когда функция (- А) является в этой точке БМ. Обозначая ее через 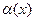(т.е. 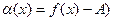приходим к следующему представлению функции в некоторой окрестности точки *.

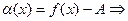
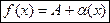при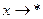

Свойства БМФ.

I. Алгебраическая сума двух БМФ при некотором стремлении есть БМФ при том же стремлении.

Пусть 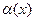, 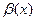- БМФ при . Это значит, что

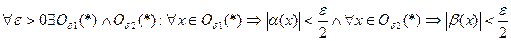
положим 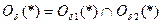, тогда очевидно, что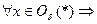 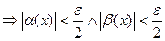и следовательно 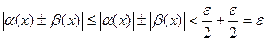т.е.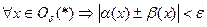

Ясно, что по индукции теорема легко распространяется на любое конечное число слагаемых.

II. Произведение ограниченной функции в некоторой окрестности точки * на БМФ при 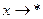есть БМФ при .

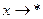Пусть - ограниченная функция в некоторой окрестности 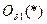, т.е.: 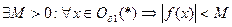Пусть далее 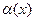- БМФ при 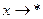, т.е.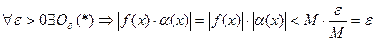

Следствия

1) Если = С=const, то: 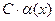- БМФ при 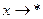где 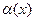- БМФ при .

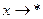2) Т.к. функция, имеющая конечный предел при некотором стремлении ограничена в некоторой окрестности этого стремления, то произведение такой функции на БМФ при том же стремлении есть БМФ при том же стремлении. В частности, если эта функция сама является БМ то заключаем, что произведение двух БМ есть БМ.

Этот последний результат легко обобщается по индукции на любое конечное число сомножителей.

Теорема. (об арифметических операциях с функциями, имеющие пределы).

Пусть функции и 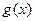имеют в точке * пределы А и В соответственно, тогда функции 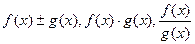так же имеют в т. * пределы соответственно равные: 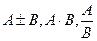(в случае частного считаем, что ).

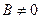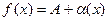
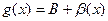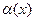Пользуясь условиями теоремы и представлением функции, имеющей предел в точке * в виде суммы некоторого предела и БМФ, имеем , где и 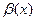- БМФ при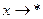

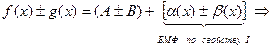
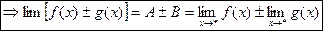
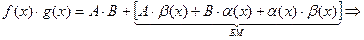
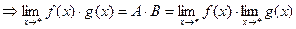
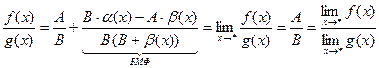где ,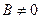

Следствия

1) Теорема по индукции распространяется на любое конечное число слагаемых или сомножителей.

2) 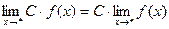где С=const

3)

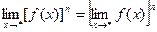
ББФ. Их связь с БМФ.

Определение

Функция называется ББ при данном стремлении, если для:

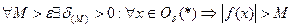пишут: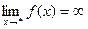

Если 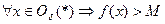, то пишут 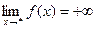, если же 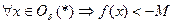, то пишут .

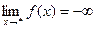Между ББФ и БМФ в точке * имеется тесная связь, которая выражается теоремой.

Теорема:

Если функция - БМФ в точке * и в некоторой окрестности точки * , то функция 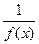ББФ в точке *.

Выберем произвольно 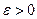, тогда (найдется)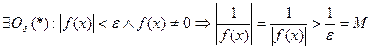

Аналогично доказывается, что справедлива и обратная теорема:

Дата добавления: 2014-01-11