Определение. Функция называется дифференцируемой в точке х0, если её приращение в этой точке имеет вид:

Функция 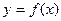называется дифференцируемой в точке х₀, если её приращение в этой точке имеет вид:

(4)

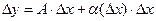
где: А - постоянное число

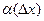- бесконечно малая при .

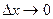Теорема

Для того чтобы функция f(x), была дифференцируема в точке х₀ необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Док-во: Пусть функция f(x) дифференцируема в точке x₀, тогда имеет место равенство (4). Считая 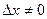, из (4) получим:

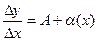
переходим к пределу при :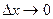

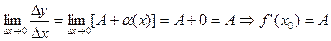, т.е. в точке х₀ существует конечная производная.

Обратно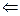

Пусть в точке х₀ функция имеет конечную производную . Обозначим её А, она равняется:

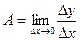, - откуда

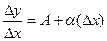, где 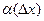- БМ при .

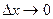Умножая обе части на последнее уравнение, приходим к уравнению (4), т.е. f(x) в точке х₀ дифференцируема. q.e.d.

Таким образом, дифференцируемость функции в точке и существование в этой точке её конечной производной - понятия равносильные (для функции многих переменных это будет не так).

Непрерывность дифференцируемой функции

Предположим, что функция f(x) производную f’(x₀).

Докажем, что функция f(x) непрерывна в точке х₀

Док-во: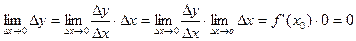

q.e.d.

Итак, дифференцируемость функции в точке влечёт её непрерывность в этой точке. Другими словами, непрерывность является необходимым условием дифференцируемости. Обратное же утверждение (непрерывность есть достаточное условие) не всегда верно.

Достаточно рассмотреть .

Эта функция, очевидно, непрерывна в точке х=0, но не дифференцируема в этой точке, т.к.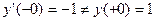

Не дифференцируемость функции в точке геометрически означает отсутствие касательной к графику функции в соответствующей точке.

Основные правила дифференцирования

1. Производная константы равна 0:

Утверждение тривиально, т.к. в любой точке х приращение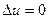

2. Пусть u(x) и v(x) дифференцируемы в т. х, тогда функции 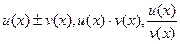также дифференцируемы в точке х:

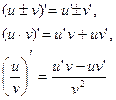
(в случае частного, считаем 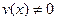).q.e.d.

Док-во:

q.e.d.

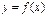Аналогично для левой верхней кривой

устанавливаются пределы

Вертикальные асимптот ы.

Предположим, что в точке x=a по крайней мере один из односторонних пределов функции f(x) бесконечен:

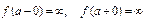(А)

тогда точка M(x,f(x)) графика функции y=f(x) удаляется по этому графику в бесконечность, а её расстояние от прямой x=a стремится к нулю. Следовательно, согласно определению асимптоты, прямая x=a является асимптотой (вертикальной) кривой y=f(x). Очевидно, что обратно, если прямая x=a является асимптотой кривой y=f(x), то хотя бы одно из условий (А) выполняется.

Дифференциальное исчисление функций одной переменной.

Производная.

Пусть функция f(x) определена на некотором промежутке X и точки x₀ и

x₀ +Dx лежат на этом промежутке

Определение 1:

Производной функции в точке x₀ называют предел (если он существует и конечен):

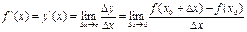
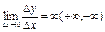
Если в точке x₀ выполняется условие:

то говорят, что функция y=f(x)имеет в точке x₀ бесконечную производную.

В отличии от бесконечной производной введённая выше производная называется конечной.

Определение 2:

Говорят, что функция y=f(x)имеет в точке x₀ правую (resp. левую) производную, если существует предел:

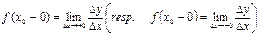Каждая из односторонних производных может быть бесконечностью(определённого знака)

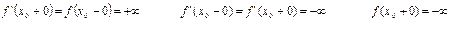
ЛЕКЦИЯ №

……………………………………………………………………………………………

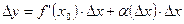где 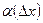- б.м. при .

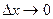Это равенство справедливо при всех достаточно малых, поэтому выберем такое , которое соответствует приращению 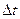аргумента функции . Поделим обе части предыдущего равенства на 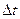и перейдем к пределу при . доказываем существование левой части уравнения. Доказательством этого будет существование предела конечного справа. Заметим, что в силу диф. функции в точке 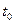она будет непрерывна в этой точке. Следовательно 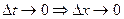. Рассмотрим предел в правой части последнего равенства:

Таким образом предел справа 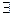и конечен, предел слева, который по определению производной равен производной функции 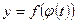в точке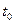

Окончательно: .

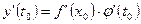Примечание.

Теорема доказана для сложной функции имеющей лишь один промежуточный аргумент. Однако последних может быть много, но правило диференц. Будет прежним.

Пример:

Пусть: y=f(u), u=u(v), v=v(t), тогда y(t)=f’(u)·u’(v)·v’(t).

Правила дифференцирования обратной функции.

Дата добавления: 2014-01-11