Редукция графа

JScript

function foo(x) {

if (x==null) // если список пуст,

then new Array[x,3] //то результат- пара х,3

else 4 //,иначе 4

}

Расширенное λ - исчисление.

(λх(if x(@

(@ cons x).

(quote 3))

(quote 4))

cons ab →(a,b)

head (cons ab) →a

tail (cons ab) →b

Любая программа может быть представлена ее синтаксическим деревом разбора.

Так как в “чистом” λ-исчислении всего две операции: λ и @, то будем в дальнейшем их использовать.

Пример. (λх.+х3)4

1-ый способ 2-ой способ

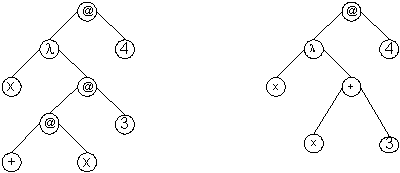
Здесь меняем все свободные вхождения х на 4

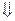
В качестве примера свернем это дерево разбора

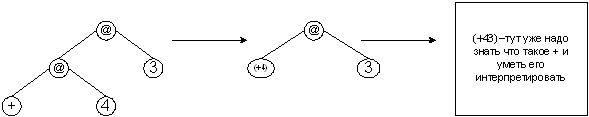
Определение:

Аппликативный порядок редукции - такой порядок редукции, который предписывает свертывать самый левый из самых внутренних редексов.

Определение:

Нормальный порядок редукции - порядок редукции, который предписывает

свертывать самый левый из самых внешних редексов.

Пример. А: λх. If x≠ 0 then x else 3/Ø. Вычислим А от 4

(Это откровенная ошибка)

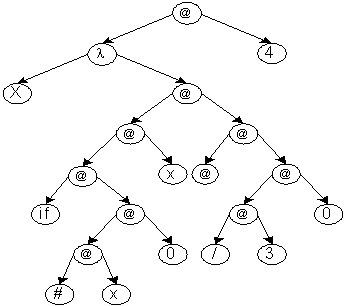
При аппликативном порядке редукции мы

получим ошибку.

При аппликативном порядке вычисляются

все аргументы функции, а уже затем – сама функция.

При нормальном порядке редукции аргументы

вычисляются по мере надобности.

При редуцировании графа мы будем пользоваться

нормальным порядком редукции.

Алгоритм редукции графа (РГ)

Редукция графа будет осуществляться циклически.

Повторить:

Спускаемся по левой ветви графа до первой вершины, которая не является аппликацией, т.е. не помечена символом @.

Если эта вершина является корнем графа, то все выражение, находится в нормальной форме, значит окончание вычислений. Если она не является корнем, то она должна являться примитивной функцией либо аппликацией и у нее должны быть все необходимые аргументы (в противном случае ошибка). Мы рекурсивно применяем алгоритм для всех поддеревьев, являющихся аргументами.

Если текущая вершина является λ- вершиной, то рассматриваем следующие варианты:

1. она является корнем графа, значит выражение в нормальной форме.

2. если она не является корнем, то над ней может быть только аппликация @ и мы на место формального параметра λ-абстракции подставляем второе выражение из правой ветви аппликации. При необходимости это поддерево копируется.

Пример. (λх.+хх)7

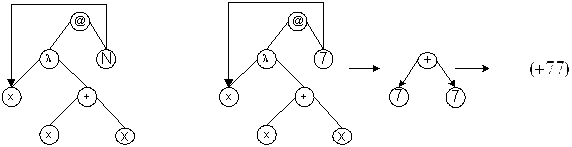
(λху.+ху)3((λх.х)4)

Дата добавления: 2014-01-11