Суперкомбинаторы

Определение:

Суперкомбинатором А арности n называется λ-выражение вида:

λх₁…х_n.Е, где на Е наложены следующие ограничения:

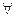λ-абстракция в Е является суперкомбинатором, Е не является λ-абстракцией,

А не содержит свободных переменных, при этом n≥0 (например, 3 (const) - это суперкомбинатор, арность n = 0).

Пример:

3 - суперкомбинатор арности 0, Е=3

λху.+ху – суперкомбинатор арности 2

λх.+((λу.у)3)х n=1

λх.+(λу.+ху)3 не является суперкомбинатором, т.к. есть внутренняя λ-абстракция, которая содержит свободную переменную.

Вычислитель возьмет программу и начнет строить правила получения результата в виде супкркомбинаторов, далее будет он применять эти правила к аргументу.

Название суперкомбинаторов принято начинать со знака $.

λху.+ху

$Аab = +ab

Если этот суперкомбинатор применить к числам, то получается $A23, что также является суперкомбинатором.

$ Prog - самый верхний суперкомбинатор, позволяющий вычислить функцию.

Так как известно, что у суперкомбинаторов фиксированная арность, то вычислить, например, $A2 невозможно - не хватает аргументов.

┌──_↓^$B

λху.+ху=(λzу.+zу)x λх.+((λzу.+zy)x)3 теперь мы получили суперкомби-

^↑───┘ └──_$Bx──┘

натор (все λ-абстракции, которые выражение содержит, являются суперкомбинаторами).

Переходы такого вида называются введением экстра-параметра.

Алгоритм приведения λ-выражения к суперкомбинаторному виду

До тех пор пока в λ-выражении есть λ-абстракция. (Цикл While).

1.Выбирать λ-абстракцию, не содержащую других λ-абстракций (т.е. внутреннюю).

а) она является суперкомбинатором. Припишем ей некоторое имя и заменим ее вхождение этим именем.

б) не является суперкомбинатором, значит, содержит свободные переменные. Вынесем все свободные переменные в качестве экстра-параметров. Припишем получившейся λ-абстракции некоторое имя и заменим ее вхождение этим именем с соответствующими экстра-параметрами.

Пример.

λх.+((λу.+ху)3)х)4 = (λх.+((λz.λy +zy)x3)x)4 = { λz.λy.+zy=$A; $Aab=+ab} =

= (λх.+($Ax3)x)4 = {$Ba = +($Aa3)a} = $B4 = {$Prog=$B4} = $Prog

По λ-выражению получили набор суперкомбинаторов, по которому можем посчитать это выражение.

Определение.

Пусть $А - суперкомбинатор арности n, тогда его аппликация к n аргументам называется комбинаторным редексом.

Определение.

Суперкомбинатор арности 0 называется константной аппликативной формой.

Суперкомбинаторный редекс можно сворачивать, только если имеются все аргументы.

Пример. λху.-yх = λх.(λy-ух) = λх.+((λz.λy.-yz)x) = λх.$Yx = $X = $Y

$Yxy = -yx Устранение избыточных параметров.

$Xx = $Yx - эта строчка избыточная; по правилу (η) имеем:

$X = $Y (η)- редукция (λх.Fx=F(x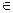F))

Дата добавления: 2014-01-11