Методы расчета поля взрыва в газах и жидкостях

В газовой динамике движение газа рассматривается как движение сплошной Среды, заполняющей все исследуемое пространство без образования пустот. Обычно параметры газа в разных точках пространства существенно отличаются друг от друга и такой газ является неравновесным. В классической термодинамике параметры неравновесного термодинамического тела (газа) вообще не подлежат рассмотрению. Поэтому в газодинамике важным является понятия элемента сплошной среды, объем которого настолько мал, что его можно считать точкой и настолько велик, чтобы содержащихся в нем частицу хватило для введения среднестатистических параметров газа. Данные элементы среды принято считать равновесными и для описания изменения их состояния за счет деформации и теплообмена можно применять уравнения равновесной термодинамики.

Таким образом движение газа можно рассматривать как механическое перемещение элементов среды изменяющих свое термодинамическое состояние.

Движение элементов среды описывается с помощью двух уравнений механики, отражающих законы сохранения массы и импульса, которые в газодинамике называются уравнениями неразрывности и количества движения.

Изменение состояния выделенных элементов описывается с помощью уравнения состояния и первого закона термодинамики, выражающего собой закон сохранения энергии. Обычно это уравнение преобразуется в уравнение изменения кинетической и внутренней энергии и в газовой динамике называется уравнением энергии.

Таким образом три дифференциальных уравнения, отражающих законы сохранения массы, импульса и энергии и алгебраическое уравнение состояния, составляют полную систему уравнений, позволяющих при известных начальных и граничных условиях определить параметры состояния газа (давление, температуру и плотность) и вектор скорости газа в каждой точке исследуемого пространства в каждый момент времени.

При изучении движения сплошной среды используются два метода: метод Лагранжа и метод Эйлера.

В методе Лагранжа отдельные частицы рассматривают как материальные точки, сплошь заполняющие некий вещественный объем. Изучение движения заключается в определении скорости, ускорения частиц и параметров состояния газа как функции времени и в исследовании изменения их при переходе от частицы к частице.

При таком подходе координаты (x, y, z) любой частицы жидкого объема в момент времени t можно рассматривать как функции времени и начального положения той же частицы (x_0, y_0, z₀):

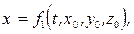
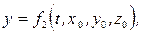
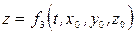
Вместо декартовых координат 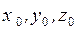можно взять любые три величины 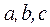связанные с 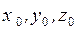однозначными зависимостями, тогда x, y, z можно представить в виде функций от переменных Лагранжа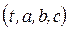. Составляющие скорости и ускорения определяются как первые и вторые производные от координат:

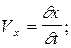
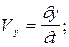
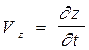
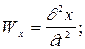
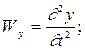
где 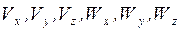–– проекции скорости 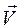и ускорения 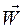на оси x, y, z.

В методе Эйлера следует за изменением параметров газа в каждой отдельной точке исследуемого пространства то есть наблюдают за изменением во времени параметров движения частицы (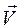,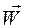), проходящей через фиксированную точку пространства и за изменением их при переходе из одной тоски пространства в другую.

Таким образом при таком подходе скорость, ускорение, плоскость и другие параметры частиц будут функциями времени и координат:

,

,

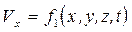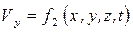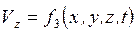
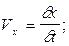
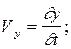
Для каждой частицы жидкости 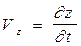, где ; ; .

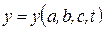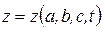При определении ускорения в переменных Эйлера надо учитывать как изменение скорости в данной тоске во времени, так и то, что через данную тоску проходят разные частицы. То есть, если частица в момент времени 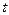имела координаты 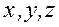и скорость 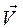, то за время 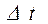она переместиться в положение , , 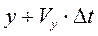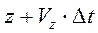и скорость ее станет

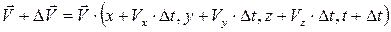
Тогда ускорение, характеризующее изменение скорости вдоль траектории движения частицы определится:

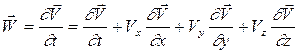
Дата добавления: 2014-01-11