Законы сохранения на фронте прямых и косых ударных волн

ОСНОВЫ ТЕОРИИ УДАРНЫХ ВОЛН

Ударные волны играют исключительно важную роль в механизме рас­пространения детонационных волн и представляют большой интерес при изучении механического действия взрыва в различных средах.

Теория ударных волн была создана еще во второй половине XIX века главным образом трудами Римана, Ренкина, Гюгонио. Первые иссле­дования ударных волн, с учетом теплопроводности, были проведены Ренкиным, который вывел для них основные дифференциальные уравнения. Одна­ко систему этих уравнений пока что удалось решить для частного случая — стационарного плоского скачка уплотнения. Основные зависимости для ста­ционарных волн можно также получить непосредственно путем приме­нения основных законов сохранения, не прибегая к интегрированию диффе­ренциальных уравнений. Пе­рейдем к выводу основных уравнений тео­рии ударной „волны.

Предварительно рассмотрим общие условия во фронте произвольной, не одномерно движущейся ударной волны. Фронт ударной волны можно рассматри­вать как поверхность, на которой претер­певают разрыв непрерывности параметры, характеризующие состояние и движение среды.

Для вывода основных соотношений на поверхности разрыва в самом общем случае неустановившихся движений сре­ды рассмотрим какой-либо элемент по­верхности разрыва в течение бесконечно малого промежутка времени. Рассмотрение проведем в прямоугольной системе координат, движущейся вместе с элементом, причем ось х направим по нормали к поверхности изучаемого элемента (рис. 4.1).

На поверхности разрыва должны выполняться основные законы сохра­нения: массы, количества движения и энергии.

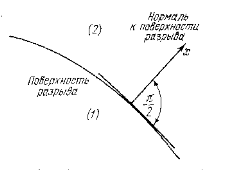
Рис. 4.1. К выводу зависимостей на поверхности разрыва.

Из закона сохранения массы вытекает, что на поверхности разрыва должен быть непрерывным поток среды через рассматриваемый элемент поверхности. Поток среды, отнесенный к единице площади поверхности раз­рыва, есть 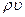, где 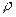— плотность среды, а 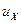— компонента скорости ее потока по оси х. Поэтому, обозначив индексами 1,2 соответственно состояние невоз­мущенной и возмущенной среды, т. е. состояния среды по обе стороны от по­верхности разрыва, можем написать закон сохранения массы (на поверхности разрыва) в виде

(4.1.1)

Закон сохранения потока количества движения запишется в следующем виде. Непрерывность x-компоненты потока количества движения соответственно будет определяться соотношениями

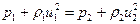(4.1.2)

Непрерывность y-компоненты и z-компоненты потока количества движения соответственно будет определяться соотношениями

(4.1.3)

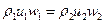(4.1.4)

Условие непрерывности потока энергии, выражающее закон сохранения энергии, будет иметь вид

(4.1.5)

(4.1.6)

где ,— полные скорости среды, — энтальпия, или тепло­содержание, среды.

Учитывая условие (4.1.1), можно соотношение (4.1.5) написать так:

(4.1.7)

К этим шести уравнениям можно добавить уравнение состояния среды

(4.1.8)

которое предполагается известным.

Уравнения (4.1.1) — (4.1.4), (4.1.6) — (4.1.8) полностью определяют условия на поверхности разрыва. По этим семи уравнениям, зная параметры состояния невозмущенной среды, можно определить , харак­теризующие движение и состояние возмущенной среды по другую сторону поверхности разрыва.

Анализируя выведенные соотношения, можно прийти к следующим выво­дам. В случае, когда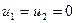, через поверхность разрыва отсутствует поток среды; при этом из (4.1.2) следует, что 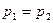, т. е. давления по обе сто­роны поверхности разрыва одинаковы. Плотности же и тангенциальные компоненты скорости и в этом случае могут иметь любые значения с обеих сторон поверхности разрыва.

Если тангенциальные компоненты скорости (хотя бы одна из них) не рав­ны между собой по обеим сторонам разрыва, то такой разрыв называется гангенциалъным. При этом плотности (энтропии) могут быть как одинаковыми, так и различными по обеим сторонам поверхности разрыва. Если же и , а 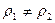такой разрыв называется особым.

Если поток среды через поверхность разрыва существует, то

(4.1.9)

При этом из уравнений (4.1.1), (4.1.3), (4.1.4) следует, что

(4.1.10)

т. е. тангенциальные компоненты скорости непрерывны на поверхности разрыва. В этом случае давление, плотность и другие термодинамические параметры состояния среды действительно испытывают скачок на поверхности разрыва, как это очевидно из выведенной системы уравнений, которые для данного случая принимают вид

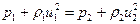
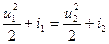(4.1.11)

В тех случаях, когда , a и 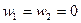, поток среды движется по нормали к поверхности разрыва, и мы будем иметь дело с прямой ударной волной. Если же 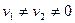и 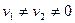, то мы будем иметь пространственную косую ударную волну; если же одна из тангенци­альных компонент скорости равна нулю, то такая волна будет плоской и на­зывается просто косой ударной волной. Заметим, что выведенные нами соот­ношения являются формально общими для поверхности разрыва любой формы. Поверхность разрыва, как уже было сказано, есть фронт ударной волны, скорость распространения которого D по определению направлена по норма­ли к поверхности. Всегда можно выбрать такую систему координат, чтобы собственное движение поверхности разрыва происходило по нормали к ней. Такую систему координат, в отличие от той, в которой фронт ударной волны (данный элемент фронта) покоится, будем называть неподвижной. В непод­вижной системе координат скорости и будут иметь соответственно зна­чения

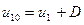
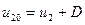(4.1.12)

и уравнения (4.1.11), если и 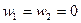, примут вид

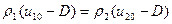
(4.1.13)

4.2. Связь между параметрами на фронте прямой ударной волны

а) Идеальная среда

Для вывода уравнений, связывающих параметры до и после ударного сжатия, удобно воспользоваться следующей схемой.

Пусть мы имеем длинную жесткую трубу с сечением F. В трубе находится покоящаяся идеальная среда с постоянными параметрами P₁, r ₁, c₁, E₁, слева расположен плоский поршень. Пусть сначала поршень поко-

ится, а затем в начальный момент времени t = 0 мгновенно приобретает некоторую скорость u2 и перемещается с этой скоростью вправо, сжимая находящуюся перед ним среду. Вправо от поршня пойдет ударная волна со скоростью D (рис. 4.2). Найдем связь между неизвестными величинами: парамет-

Рис. 4.2. Расчетная схема

рами среды в ударно-сжатой области (за фронтом ударной волны) и параметрами невозмущенной среды. Для этого воспользуемся законами сохранения массы, импульса и энергии. Параметры невозмущенной среды P₁, r ₁, c₁, E₁ и скорость поршня u₂, с которой совпадает скорость среды за фронтом ударной волны, будем считать известными.

К моменту времени t в трубе с сечением F движение охватывает массу среды, равную r ₁FDt. Но к моменту времени t эта масса среды занимает уже объем (D-u₂)tF, в котором плотность среды равна r ₂, то есть удовлетворяется условие

Сократив одинаковые члены в правой и левой частях, запишем закон сохранения массы при переходе через фронт ударной волны

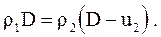(4.2.1)

Это уравнение представляет собой уравнение сохранения массы на фронте ударной волны.

Масса газа r ₁FDt приобретает количество движения r ₁FDtu₂, которое по закону Ньютона равно импульсу сил давления. Результирующая сила, действующая на сжатую среду, равна (FP₂-FP₁), тогда импульс силы, действующей на сжатую среду, будет равен (FP₂-FP₁)t. Приравняем изменение количества движения массы среды, находящегося за фронтом ударной волны, и импульс силы, действующей на эту массу

r ₁FDtu_{2 =} (FP₂-FP₁)t.

Сократим в обеих частях полученного равенства площадь сечения трубы F и время t. Получим закон сохранения импульса для фронта ударной волны

(4.2.2)

При адиабатическом сжатии среды изменение полной энергии газа равно работе внешних сил. До ударного сжатия единица массы среды имела внутреннюю энергию Е₁, после ударного сжатия энергия единицы массы стала . Изменение полной энергии всей массы ударно сжатой среды равно

.

Внешняя сила, сжимающая среду, равна P₂f, и действует на пути u₂t. Учитывая все это, получим соотношение

Преобразовав это выражение, получим закон сохранения энергии для ударной волны

(4.2.3)

Преобразуем это уравнение к виду, удобному для практического пользования. Для этого исключим скорость из уравнения (4.2.3). Из уравнений (4.2.1) и (4.2.2) определим D и u₂

(4.2.4)

где 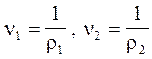. Подставим полученные выражения для D и u₂ в (4.2.3)

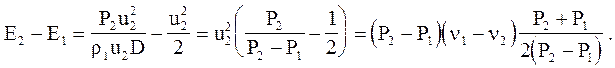
Окончательно уравнение сохранения энергии для ударной волны примет вид

(4.2.5)

Кроме трех уравнений (4.2.1), (4.2.2), (4.2.5), выражающих сохранение массы, импульса и энергии, необходимо еще знать термодинамическое состояние среды за фронтом ударной волны. Обычно оно задается уравнением

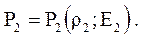(4.2.6)

Система четырех уравнений (4.2.1), (4.2.2), (4.2.5), (4.2.6) связывает пять параметров на фронте ударной волны P₂, u₂, r ₂, D, E_4.2. Для того, чтобы решить эту систему, достаточно знать один параметр (любой из пяти, например, u₂ или D), тогда остальные определяются при помощи этой системы. Для определения температуры среды при ударном сжатии необходимо знать уравнение состояния в виде

(4.2.6а)

б) Прочная среда

Если в трубе (см. рис. 4.2.2) находится не идеальная среда, а сжимаемая прочная среда, то соотношения между параметрами до и после ударного сжатия устанавливаются так же, как для идеальной среды. Пусть перед фронтом ударной волны в твердом теле перемещается упругая волна с параметрами s _1а, r _a, u_a, E_a, тогда на основе законов сохранения массы, импульса и энергии получим следующие соотношения:

(4.2.7)

где - параметры на фронте ударной волны: соответственно скорость ударной волны, массовая скорость, напряжение в направлении оси ox, плотность, удельная энергия. Для плоской ударной волны к этим уравнениям, согласно теории прочности, надо добавить: уравнения состояния P = P(r, E) и P = P(r,T); зависимость интенсивности напряжений s_i от интенсивности деформации e_i для данной амплитуды ударной волны s_i = s_i(e_i); зависимость напряжения s₁ от среднего давления P и элемента девиатора напряжений S₁: s₁ = - P + S₁, а также

Следовательно, к (4.2.7) надо добавить:

(4.2.7а)

Девять уравнений в системах (4.2.7) и (4.2.7а) содержат десять неизвестных параметров: D, r, u, E, P, s₁, s_i, e_i, T, S₁. Один из этих параметров должен быть задан, а остальные определяются из уравнений (4.2.7), (4.2.7а).

Если среда идеальная и до ударного сжатия находится в покое, то полагая в этих уравнениях u_а = 0, s_1а = - P₁, r _а = r ₁, s₁ = - P₂, S₁= 0, s_i = 0, получим уравнения (4.2.1), (4.2.2) и (4.2.5).

в) Совершенный газ

В случае совершенного газа система уравнений (4.2.1), (4.2.2), (4.2.5) и (4.2.6), связывающая параметры газа (без учета процессов диссоциации и ионизации) на фронте ударной волны, значительно упрощается.

Первые два уравнения (4.2.1), (4.2.2), выражающие закон сохранения массы и закон сохранения импульса, в случае совершенного газа остаются без изменения

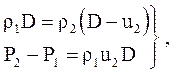(4.2.8)

поскольку законы сохранения массы и импульса не зависят от термодинамических свойств газа.

Уравнение сохранения энергии с учетом того, что для совершенного газа справедливо соотношение запишется в виде

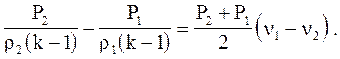(4.2.9)

Четвертое уравнение, связывающее давление, плотность и внутреннюю энергию газа P₂=P₂(r ₂, E₂), в данном случае не требуется, так как оно в виде уже входит в уравнение (4.2.9).

Если нас интересует температура, то в систему вводится уравнение состояния

P₂ = P₂(r ₂, T₂).

Для совершенного газа:

P₂ = r ₂RT_4.2. (4.2.10)

г) Газ с учетом процессов ионизации и диссоциации

В сильной ударной волне значительно повышаются температура и внутренняя энергия газа, а благодаря развитию процессов диссоциации и ионизации - и число частиц в среде. В воздухе процессы диссоциации до T = 1300^°К малы и ими можно пренебречь при любых плотностях 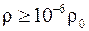(где г/см³ - плотность воздуха при нормальных условиях). Заметный процесс диссоциации, то есть распад молекул кислорода O₂ и азота N₂ на атомы, начинается с 2000^°К (при нормальном давлении). Этот процесс практически заканчивается при 6000^°К. Заметная ионизация воздуха начинается при 6000^°К, при этом происходит отрыв внешних электронов от атомов. То есть для каждой амплитуды ударного сжатия, характеризующейся параметрами T₂, P₂, r ₂, E₂, S₂, состав воздуха, вследствие процессов диссоциации и ионизации, различен. Поэтому термодинамические свойства воздуха до и после ударного сжатия неодинаковы. Так, различны показатели изоэнтропы и молекулярный вес воздуха до и после ударного сжатия. В этом случае на основе термодинамических расчетов необходимо определять состав воздуха при каждом определенном ударном сжатии. В основе расчетов параметров ударных волн лежит система уравнений

(4.2.11)

Задаваясь, например, температурой T₂, определяют остальные параметры ударной волны P₂, r ₂, u₂, D при условии, что на основе термодинамических расчетов с учетом процессов диссоциации и ионизации воздуха известны уравнения состояния E₂ = E₂(r ₂,T₂) и P₂ = P₂(r, T₂). Исходными для этих вычислений служат данные о потенциалах диссоциации и ионизации и об энергетических уровнях частиц воздуха.

В настоящее время существуют подробные таблицы с параметрами ударных волн в воздухе, которыми удобно и просто пользоваться на практике. Такие таблицы охватывают интервал температур от 200 до 3 × 10⁶ °К и плотности от 30 r ₀ до 10^-6 r ₀, и дают информацию об ударных волнах в воздухе на различных высотах h над уровнем моря от h = 0 до h = 100 км.

Ниже приведена таблица для параметров ударных волн на h = 0 км. При пользовании ею необходимо задать один из параметров, например Т₂, или P₂, или D, тогда остальные определяются из табл. 4.1. В табл. 4.1 даны также эффективные значения показателя изоэнтропы , скорость звука с, энтропия S₂ и др.

Дата добавления: 2014-01-11