Ударная адиабата

Параметры ударной волны связаны между собой законами сохранения массы и импульса (4.2.1), (4.2.2), которые не зависят от термодинамических свойств среды:

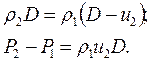
Зависимость между любыми двумя параметрами на фронте ударной волны, входящими в эти уравнения, D, u₂, P₂, r ₂ называется ударной адиабатой, или адиабатой Гюгонио. Эта ударная адиабата зависит также от начальных параметров среды P₁, r ₁. Она имеет вид

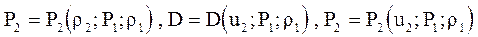и т.п.

Каждая точка на ударной адиабате соответствует определенному состоянию ударной волны, то есть это уравнение представляет собой геометрическое место точек возможных состояний на фронте ударной волны. Конкретный вид уравнения ударной адиабаты среды может быть получен из полной системы уравнений на фронте ударной волны. Для этого необходимо из уравнения энергии (4.2.5) и известного уравнения состояния (4.2.6) исключить внутреннюю энергию Е₂, в результате получим уравнение в виде

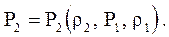
Такой способ получения адиабаты пригоден только в том случае, если известно уравнение состояния среды P₂= P₂(r ₂, E₂), например, для совершенного газа, где 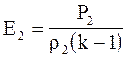. Для любой идеальной среды получить таким образом ударную адиабату нельзя, поскольку уравнение состояния обычно неизвестно. В настоящее время для твердых и жидких тел ударные адиабаты определяют экспериментально, а используя эту экспериментальную адиабату, можно вычислить уравнение состояния (см. п.4.11).

Рассмотрим ударную адиабату для совершенного газа. Наиболее простой вид имеют формулы для ударной волны в случае совершенного газа. Подставим в уравнение энергии (4.2.5)

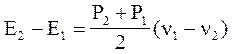
соотношение, справедливое для совершенного газа,

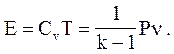
В результате получим уравнение ударной адиабаты в виде

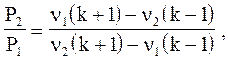(4.3.12)

а для соотношения плотностей

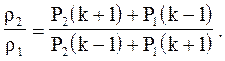(4.3.13)

Ударная адиабата представляет собой кривую в плоскости P2, r 2, проходящую через точку начального состояния P1, r 1. Эта кривая изображена на рис. 4.3.3. Из уравнения (4.3.13) видно, что при бесконечном увеличении давления P2 за фронтом ударной волны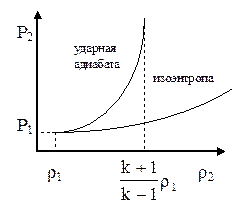

Рис. 4.3. Изоэнтропа и ударная адиабата

(случай очень большой амплитуды ударной волны) плотность газа не увеличивается беспредельно, а стремится к определенному предельному значению. Это предельное значение легко вычислить, если в уравнении адиабаты Гюгонио (4.3.13) сделать следующие преобразования:

(4.3.14)

Предел, к которому стремится правая часть этого выражения при P₂ ® ¥, равен

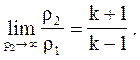(4.3.15)

Теперь подсчитаем, до какой предельной плотности можно сжать газ при однократном прохождении ударной волны. Эта предельная плотность равна

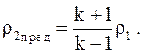(4.3.16)

Как видно из (4.3.15) и (4.3.16), предельное сжатие в ударной волне зависит только от показателя адиабаты и равно

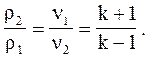(4.3.17)

Для идеального газа с показателем адиабаты k = 1,4 (что соответствует воздуху при нормальных условиях) предельное сжатие равно 6, при k = 1,2 (ионизированный и диссоциированный воздух) оно равно 11. Возникает вопрос: почему нельзя ударной волной газ сжать до плотности, большей r _2пред? (см. п.4.3.5.).

Сравним теперь изоэнтропическое и ударное сжатие. Уравнение изоэнтропы имеет вид

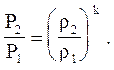(4.3.18)

Как видно из этого уравнения, при изоэнтропическом сжатии газ можно сжать во сколько угодно раз, то есть можно увеличивать плотность до бесконечности при беспредельном увеличении давления. Сравнение ударной адиабаты и изоэнтропы приведено на рис. 4.3 и 4.4.

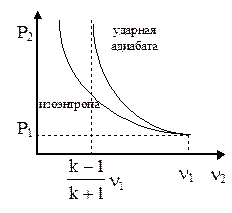Рис. 4.4. Изоэнтропа и ударная адиабата

Дата добавления: 2014-01-11