Тема: Простые и сложные проценты

S = P+I (1.1), где

S – наращённая сумма,

P - первоначальная сумма,

I – начисленные проценты.

Проценты I за весь срок ссуды соответственно будут вычисляться как:

I = P_ni (1.2), где

n – срок ссуды (в годах),

i – процентная ставка наращения.

S = P_(1+ni) (1.3), где (1+ni) – множитель наращения простых процентов.

Пример: ссуда в 25 000 сроком на 0,7 года под простые проценты 18% годовых, определить проценты и наращённую сумму.

Решение:

P = 25 000

n = 0.7

i = 18%

I -? S -?

I = 25 000*0.7*0.18 = 3150

S = 25 000 + 3150 = 28150

Срок ссуды рассчитывается обычно по формуле:

n = t/К (1.4)

где

t – число дней ссуды,

К – временная база или число дней в году

2 типа временных баз:

1) К = 360 – обыкновенные %

2) К = 365/366 – точные %

При расчёте срока ссуды при начислении по простым процентам use 3 метода:

1. Точные проценты с точным числом дней ссуды 365/361. Кол-во дней ссуды рассчитывается точно по календарю: первый и последний дни принимаются за один. Временная база К = 365 или 366. Этот метод применяется, как правило, центробанком в разных странах, а также крупными коммерческими банками.

2. Обыкновенные проценты с точным числом дней ссуды 365/360, временная база берётся в 365 дней. Как правило, такой расчёт проводится в коммерческих банках.

3. Обыкновенные проценты с приближённым числом дней ссуды, то есть 360/360. Кол-во дней в каждом месяце принимается в 30. Временная база – 360. Данный метод применяется при промежуточных расчётах.

Пример: ссуда в размере 8 млн руб выдана с 28 января по 15 июня включительно, под простые проценты 22% годовых. Определить величину долга в конце срока. Решить тремя методами.

1 метод:

P = 8 млн. руб

t₁ = 28 янв

t₂ = 15 июня

i = 28% (простые)

S -?

Рассчитаем точное кол-во дней в первом и втором случае:

t = 28+31+30+31+3 (за 1 месяц от января) + 14 (от июня) +1 (общий день) = 138

Приближённое:

t = 4*30+2 (месяц январь берётся за 30 дней) +14+1 = 137

S₁ = 8 + 138/365 (t/K) * 0.22 = 8.6654248

2 случай:

S₂ = 8*(1+138/360 * 0.22) = 8.6746664

3 случай:

S₃ = 8*(1+137/360 * 0.22) = 8.6697776

Если процентные ставки нарощения изменяются во времени, то наращённая сумма будет, соответственно, вычисляться как:

S = P(1+n₁i₁+...+n_ki_k) = P(1+ 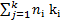) (1.5)

где n₁, n₂...n_k – временные интервалы

i₁, i₂...i_k – соответствующие интервалам ставки

При дисконтировании сумма S, кот будет выдана через срок n по ставке дисконтирования i, вычисляется современная величина или стоимость P.

P = S / (1+ni) (1.6)

D = 1 / 1+ni (1.7) – дисконтный множитель

D = S-P (1.8) – дисконт суммы S

Задача: Через 159 дней должник уплатит 8,5. Кредит выдан под 19% годовых - простые проценты. Какова первоначальная сумма долга и дисконт при условии, что временная база равна 360 дней.

S = 8,5

t = 159

i = 19%

К = 360

P -? D -?

P = 8.5 / (1+ 159/360 *0.19) = 7.84193 тыс руб

D = 8.5 – 7.84193 = 0.6587 тыс руб

Банк может учесть вексель до наступления срока платежа с дисконтом, то есть купить его у владельца по цене, которая меньше номинала, указанного в векселе. Номинал – это сумма денег, указанная на векселе, которую получит владелец при его погашении в момент наступления срока платежа. Размер дисконта при учёте по простой учётной ставке будет определяться по формуле:

D = Snd, где

d – простая учётная ставка,

n – срок от момента учёта до момента погашения.

Подставив эту формулу в формулу (1.8), получим при расчёте суммы выданной владельцу при учёте векселя:

P = S(1-nd) (1.9)

где (1-nd) – дисконтный множитель

Временная база при этом К = 360.

Соответственно, простая учётная ставка может также use и при расчёте номинала. В данном случае номинал 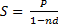(1.10).

Пример: Вексель, имеющий номинальную стоимость 8 тыс, учтён в банке по учётной ставке 18,5% годовых за 132 дня до его погашения. Определить сумму, полученную владельцем при учёте.

S = 8

i = 18.5%

t = 132

P = 8*(1-132/360*0.185) = 7.45733 тыс. руб.

В тех случаях, когда известны величина долга в начале и в конце срока ссуды, а также процентная ставка, можно определить срок этой ссуды.

Воспользуемся формулой (1.3) и выразим оттуда n:

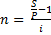(1.11)

Для простой учётной ставки срок ссуды определим из формулы (1.9):

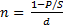(1.12)

Дата добавления: 2014-01-11