Элементы квантовой механики

Основные вопросы

Ø Гипотеза де Бройля.

Ø Корпускулярно-волновой дуализм.

Ø Принцип дополнительности.

Ø Соотношение неопределённостей Гейзенберга.

Ø Волновая функция, её статистический смысл.

Ø Уравнение Шредингера.

Ø Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими стенками.

Ø Линейный гармонический осциллятор в квантовой механике.

Ø Операторы квантовой механики, квантование физических величин, собственные значения и собственные функции.

1. Гипотеза де Бройля

«В оптике в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым способом; не делалась ли в теории вещества обратная ошибка? Не думали ли мы слишком много о картине "частиц" и не пренебрегали ли чрезмерно картиной волн?»

Луи де Бройль, лауреат Нобелевской премии по физике 1929 года

С каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ. Они связаны количественными соотношениями, аналогичными фотону:

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной λ и частотой ω волны:

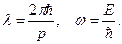
Для частиц, имеющих массу,

В нерелятивистском приближении (υ << c).

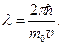
Гипотеза де Бройля основывалась на соображениях симметрии свойств материи и не имела в то время опытного подтверждения. Но она явилась мощным революционным толчком к развитию новых представлений о природе материальных объектов.

Экспериментальное подтверждение гипотезы.

1. Получение дифракционной картины при рассеивании пучка электронов кристаллом никеля. По положению дифракционных максимумов была определена длина волны электронного пучка, которая оказалась в полном соответствии с формулой де Бройля (1927 год, американские физики Клинтон Девиссон и Лестер Джермер).

2. Наблюдение дифракционной картины, возникающей при прохождении пучка электронов через тонкую золотую поликристаллическую фольгу (1928 год, английский физик Джордж Томсон).

3. Наблюдение дифракционной картины при прохождении через прибор единичных электронов (1948 год, советский физик Валентин Фабрикант).

Дифракция электронов: на установленной за фольгой фотопластинке хорошо наблюдаются концентрические светлые и темные кольца, радиусы которых изменяются с изменением скорости электронов (то есть длины волны) согласно де Бройлю:

1. Корпускулярно-волновой дуализм

«Можно сказать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна – частица. Всякое иное, более буквальное, понимание этого дуализма в виде какой-нибудь модели неправильно»

Владимир Александрович Фок

1. Принцип дополнительности

Всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни волной, ни частицей в классическом понимании. Разные свойства микрообъектов не проявляются одновременно; они дополняют друг друга, и только их совокупность характеризует микрообъект.

Принцип сформулирован в 1927 году датским физиком-теоретиком Нильсом Бором.

1. Соотношение неопределённостей

При дифракции электронов на одиночной щели более 85% их попадёт в центральный дифракционный максимум:

Угловая полуширина θ ₁ центрального дифракционного максимума находится из условия

где D – ширина щели, λ – длина волны. Это формула волновой теории.

С корпускулярной точки зрения можно считать, что при пролете через щель электрон получает дополнительный импульс p_x в поперечном направлении.

Пренебрегая 15% электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение p_x поперечного импульса равно

При прохождении электрона через щель в эксперименте его положение (координата x) определяется с точностью Δ x. При этом Δ x = D.

Точность определения p_x в момент прохождения электрона через щель равна самому значению p_x (Δ p_x ≥ p_x) или даже больше, учитывая побочные максимумы дифракционной картины.

Следовательно,

Тогда

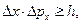
где Δ x и Δ p_x – неопределённости измерения координаты и проекции импульса.

Соотношение известно, как принцип неопределённостей Гейзенберга, открытый им в 1927 году. Он понимается как невозможность одновременно точного определения координаты и проекции импульса микрочастицы.

Аналогично можно записать:

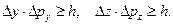
Координата и импульс являются канонически сопряжёнными величинами. Тогда принцип неопределённостей Гейзенберга можно сформулировать, как произведение неопределённостей двух сопряжённых переменных не может быть по порядку величины меньше постоянной Планка.

Время и энергия также являются канонически сопряжёнными величинами, поэтому

Это соотношение означает, что определение энергии с точностью Δ E должно занять интервал времени, равный по меньшей мере Δ t ~ h /Δ E.

1. Волновая функция

При дифракции электронов на двух щелях (аналог опыта Юнга) наблюдается их интерференция.

Подобный результат можно объяснить, если принять, что электрон, как и волна, не локализован в пространстве. Тогда описание его состояние не может ограничиваться лишь набором значений физических величин.

Полностью состояние микрочастицы в квантовой механике характеризует волновая функция, которую принято обозначать буквой Ψ (пси).

Соотношение между волновой функцией Ψ и описываемой ею частицей аналогично соотношению между световой волной и фотоном.

Волновая функция должна быть однозначной, конечной и непрерывной во всей области изменения пространственных координат.

По аналогии с уравнением плоской волны можно записать уравнение волны де Бройля для свободной частицы, движущейся вдоль оси x, в виде

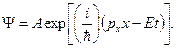
Имея зачастую комплексно-сопряжённое значение волновая функция сама по себе не имеет физического смысла.

Квадрат модуля волновой функции для какой-либо точки пространства, будучи умножен на включающий в себя эту точку элемент объёма dV, определяет вероятность dP того, что частица будет обнаружена в пределах объёма dV:

Физический смысл функции Ψ заключается в том, что квадрат её модуля даёт плотность вероятности P (вероятность, отнесённую к единице объёма) нахождения частицы в соответствующем месте пространства:

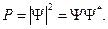
Дата добавления: 2014-01-11