Решение уравнения Шредингера для водородоподобного атома

Рассмотрим простейший атом, состоящий из электрона зарядом e, двигающегося в кулоновском поле ядра с зарядом Ze, где Z – порядковый номер элемента в Периодической системе Дмитрия Ивановича Менделеева. Такую систему называют водородоподобной. При Z =1 это атом водорода, при Z =2 – однократно ионизированный атом гелия – He⁺, при Z =2 – двукратно ионизированный атом лития – Li²⁺ и так далее.

Хотя из всех атомов Периодической системы только водород и его изотопы относятся к одноэлектронным атомам, квантово-механическое рассмотрение систем этого типа имеет фундаментальное значение. Это объясняется тем, что для атомов и ионов с одним электроном может быть точно решено уравнение Шредингера, а полученные решения служат основой для изучения всех более сложных задач о многоэлектронных атомах и даже молекулах.

Потенциальная энергия U (r) взаимодействия электрона с ядром в рассматриваемой системе равна

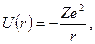
(8.1)

где r – расстояние между электроном и ядром, которое в первом приближении будем считать точечным (здесь и далее). Тогда уравнение Шредингера (ХХХ) в этом случае принимает вид

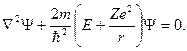
(8.2)

В представленном уравнении m должно быть приведённой массой ядра и электрона, но, учитывая факт, что электрон движется гораздо быстрее, можем говорить лишь о том, что m это его масса, не рассматривая массу ядра. Такое допущение в значительной степени упрощает поиск решения уравнения, а погрешность составляет порядка 0,05%.

Поскольку кулоновское поле ядра является центрально-симметричным, то есть зависит только от r, то решение уравнения (8.2) наиболее целесообразно проводить в сферической системе координат (связь декартовых координат x, y, z со сферическими координатами r, θ, j представлена на рисунке 1). Для этого воспользуемся следующими правилами перевода между декартовой и сферической системами координат:

Здесь dv – элемент объёма, координаты сферической системы имеют следующие интервалы: 0≤ r ≤∞, 0≤ θ ≤ π, 0≤ j ≤2 π.

Переход к сферическим координатам создаёт возможность разделения переменных в уравнении Шредингера, чего нельзя сделать при записи этого уравнения в декартовых координатах. В итоге оператор Лапласа принимает вид

(8.3)

Заменяя в уравнении (8.2) оператор Лапласа полученным оператором (8.3), приходим к выводу, что полная волновая функция, являющаяся решением уравнения Шредингера, может быть разделена на три составляющих – три функции каждой сферической координаты:

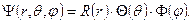
(8.4)

Мы не будем рассматривать полный ход решения, ограничимся лишь наиболее значимыми для нас моментами. Во-первых, первая составляющая – R (r) – является радиальной частью волновой функции и определяет расстояние электрона от ядра (в классической теории атома аналогом является радиус орбитали электрона), произведение двух других составляющих – Q(θ) и F(j) – представляет угловую часть волновой функции (в классическом представлении атома аналогом может служить форма и направление орбитали электрона). Во-вторых, полная волновая функции зависит от трёх целочисленных параметром: n, l и m, которые называются, соответственно, главное, орбитальное и магнитное квантовое число. При этом радиальная часть волновой функции зависит от n и l, а угловая – от l и m. Главное квантовое число n принимает значения 1, 2, 3 и так далее, орбитальное квантовое число принимает значение от 0 до n –1 при заданном значении n, а магнитное квантовое число принимает значения от – l до l при заданном значении l. Например, если n =2, то l принимает значения 0 и 1. Если l =0, то m также равно 0. Если l =1, то m принимает значения –1, 0 и 1.

Содержание

Элементы геометрической оптики. 1

Явление интерференции. 8

Тепловое излучение. 12

Корпускулярная природа света. 22

Элементы квантовой механики. 31

Квантовая механика атомов и молекул. 40

Дата добавления: 2014-01-11