Поток энергии волны

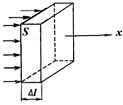При распространении волн частицы среды не переносятся вместе с волной. Процесс распространения волны в каком-либо направлении в среде сопровождается переносом энергии колебаний в этом направлении. Допустим, что S часть фронта плоской волны распространяющейся в направлении оси Ох в некоторый момент времени t (рис. 1.2). По истечении времени ∆ t фронт волны переместится на расстояние ∆ l = v ∆ t, вследствие чего частицы среды в объеме ∆ V = S ∆ l приводятся в колебательное движение. Они будут обладать энергией

∆ W = w ∆ V = wvS ∆ t,

Рис. 1.2 14.34

где w – объемная плотность энергии. Можно утверждать, что за время ∆ t среда через площадку S получила энергию wvS ∆ t. Таким образом, за единицу времени через площадку S прошла энергия

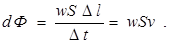
Величина dФ есть поток энергии волны через площадку S (S ориентируют перпендикулярно к направлению распространения волны). Плотностью потока энергии называют энергию, проходящую за единицу времени через единицу площадки, перпендикулярной к направлению распространения волны:

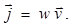(1.10)

Этот вектор называют вектором Умова и Пойнтинга. Учитывая, что 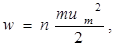где n – концентрация частиц среды, u_m = Аω – амплитуда скорости колебаний частиц среды, плотность энергии 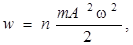а j ~ A ². Распространяющиеся волны характеризуют понятием интенсивность волны I, которая пропорциональна среднему значению плотности потока, а, следовательно, I ~ A ².

В сферической волне, вызванной точечным источником колебаний, плотность потока энергии убывает обратно пропорционально квадрату расстояния от источника колебаний. Для доказательства допустим, что источник колебаний ежесекундно отдает в окружающую среду одну и ту же энергию, равную W. Эта энергия равномерно распределяется по шаровой поверхности фронта волны S = 4π r ², поэтому через единицу площади этой поверхности в единицу времени проходит энергия

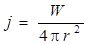, т. е. j ~ 1/ r ², а А ~ 1/ r (см. 1.9).

Дата добавления: 2014-01-11