Уравнение Шредингера

Мы уже отмечали, что если частица обладает волновыми свойствами, которыми нельзя пренебречь в рассматриваемой задаче, то поведение такой частицы нельзя описывать уравнениями классической физики. Нужны новые уравнения, которые бы учитывали наличие волновых свойств. Одно из таких уравнений было получено Шредингером в 1926 г.

Оно имеет следующий вид:

(9.1)

где 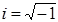- мнимая единица; m – масса частицы; U (x,y,z,t)– потенциальная энергия частицы в силовом поле, в котором она движется; - оператор Лапласа, его действие на волновую функцию сводится к взятию вторых частных производных по координатам. В левой части уравнения берется частная производная от волновой функции по времени t.

Уравнение Шредингера является основным уравнением квантовой механики, оно не выводится, его справедливость проверяется сопоставлением полученных из него результатов с опытными данными. Его значение в квантовой механике сравнимо с уравнением Ньютона в классической механике и Максвелла в электродинамике.

Обычно рассматриваются силовые поля, которые явно не зависят от времени t. Их называют стационарными полями. В таких полях потенциальная энергия частицы не зависит от времени U = U (x, y, z),а полная энергия частицы остается постоянной (W = U + W _к= const).Волновую функцию в этом случае можно представить в вида произведения координатной ее части на временную:

Для координатной части волновой функции уравнение Шредингера (его называют стационарным уравнением Шредингера) принимает вид

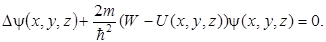(9.2)

В теории дифференциальных уравнений доказывается, что уравнения такого вида, как уравнение Шредингера имеют решения, удовлетворяющие требованиям конечности, непрерывности и однозначности не при любых значениях полной энергии W, а лишь при определенных. Эти значения энергии называют собственными значениями, а соответствующие им волновые функции – собственные функции задачи.

Решая задачу, с использованием уравнения Шредингера, находят собственные значения энергии рассматриваемой частицы и соответствующие им волновые функции, которые и позволяют определить вероятность нахождения частицы с определенной энергией в интересующей области пространства.

Дата добавления: 2014-01-11