КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип квазирегулярности
|
|
|
|
Схема гибели и размножения
Часто в системах самого различного назначения протекают процессы, которые можно представить в виде модели "гибели и размножения".
Граф состояний такого процесса показан на рис. 2.5.

увеличить изображение
Рис. 2.5. Схема "гибели и размножения"
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним "соседом" (с последующим и предыдущим состояниями соответственно).
Название модели - "гибель и размножение" - связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния ("рождение"), а стрелки влево - с убыванием номера состояний ("гибель").
Очевидно, стационарное состояние в этом процессе существует. Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках, а также в рекомендованной литературе.
Для приведенных на рис. 2.5 обозначений формулы имеют вид:
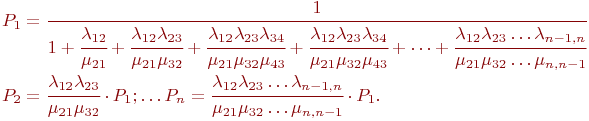
Пример 2.3. Имеется система из двух одинаковых и работающих параллельно компьютеров.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
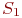 - оба компьютера исправны;
- оба компьютера исправны;
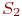 - один компьютер исправен, другой ремонтируется;
- один компьютер исправен, другой ремонтируется;
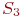 - оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
- оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
Поскольку компьютеры одинаковые, то с точки зрения надежности, неважно, какой именно компьютер неисправен в состоянии 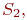 важно, что один.
важно, что один.
С учетом сказанного, ситуация моделируется схемой "гибели и размножения" (рис. 2.6).
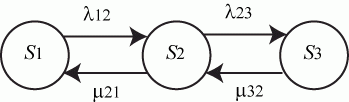
Рис. 2.6.
На рис. 2.6:
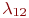 ,
, 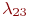 - интенсивности потоков отказов;
- интенсивности потоков отказов;
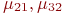 - интенсивности потоков восстановлений.
- интенсивности потоков восстановлений.
Пусть среднее время безотказной работы каждого компьютера
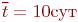 ., а среднее время восстановления одного компьютера
., а среднее время восстановления одного компьютера 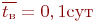 .
.
Тогда интенсивность отказов одного компьютера будет равна 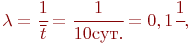 а интенсивность восстановления одного компьютера -
а интенсивность восстановления одного компьютера - 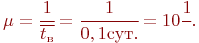
В состоянии 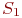 работают оба компьютера, следовательно:
работают оба компьютера, следовательно:
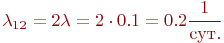
В состоянии 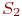 работает один компьютер, значит:
работает один компьютер, значит:

В состоянии 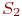 восстанавливается один компьютер, тогда:
восстанавливается один компьютер, тогда:
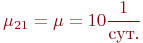
В состоянии 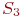 восстанавливаются оба компьютера:
восстанавливаются оба компьютера:
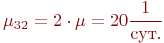
Используем зависимости (2.2). Вероятность состояния, когда обе машины исправны:
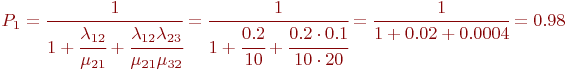
Вероятность второго состояния 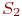 (работает один компьютер):
(работает один компьютер):
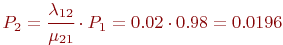
Аналогично вычисляется и 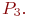 Хотя найти
Хотя найти 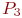 можно и так:
можно и так:
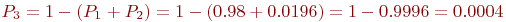
Пример 2.4. В полосе объединения работают передатчики противника. Подразделение операторов-связистов армейской контрразведки ведет поиск передатчиков по их радиоизлучениям. Каждый оператор, обнаружив передатчик противника, следит за его частотой, при этом новым поиском не занимается. В процессе слежения частота может быть потеряна, после чего оператор снова осуществляет поиск.
Разработать математическую модель для определения эффективности службы подразделения операторов. Под эффективностью понимается среднее число обнаруженных передатчиков за установленный промежуток времени.
Решение
Будем считать, что наши операторы и радисты противника обладают высокой квалификацией, хорошо натренированы. Следовательно, можно принять, что интенсивности обнаружения частот передатчиков противника и потерь слежения - постоянны. Обнаружение частоты и ее потеря зависят только от того, сколько запеленговано передатчиков в настоящий момент и не зависят от того, когда произошло это пеленгование. Следовательно, процесс обнаружения и потерь слежения за частотами можно считать непрерывным однородным марковским процессом.
Исследуемое свойство этой системы пеленгации: загруженность операторов, что, очевидно, совпадает с числом обнаруженных частот.
Введем обозначения:
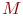 - количество операторов;
- количество операторов;
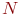 - количество передатчиков противника, полагаем
- количество передатчиков противника, полагаем 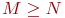 ;
;
 - среднее число операторов, ведущих слежение;
- среднее число операторов, ведущих слежение;
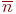 - среднее число запеленгованных передатчиков;
- среднее число запеленгованных передатчиков;
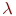 - интенсивность пеленгации передатчика противника одним оператором;
- интенсивность пеленгации передатчика противника одним оператором;
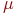 - интенсивность потока потерь слежения оператором;
- интенсивность потока потерь слежения оператором;
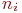 - текущая численность запеленгованных передатчиков
- текущая численность запеленгованных передатчиков 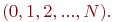
В системе пеленгации возможны следующие состояния:
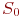 - запеленгованных передатчиков нет, поиск ведут
- запеленгованных передатчиков нет, поиск ведут 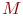 операторов, вероятность состояния
операторов, вероятность состояния 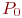 ;
;
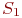 - запеленгован 1 передатчик, поиск ведут
- запеленгован 1 передатчик, поиск ведут 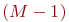 операторов, вероятность состояния
операторов, вероятность состояния 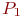 ;
;
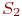 - запеленгованы 2 передатчика, поиск ведут
- запеленгованы 2 передатчика, поиск ведут 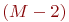 операторов, вероятность состояния
операторов, вероятность состояния 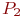 ;
;
…
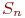 - запеленгованы
- запеленгованы 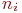 передатчиков, вероятность
передатчиков, вероятность 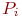 ;
;
…
 - запеленгованы
- запеленгованы 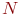 передатчиков, вероятность
передатчиков, вероятность 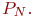
Цель моделирования - 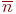 - достигается вычислением:
- достигается вычислением:
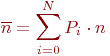
Как и в примере 2.3 полагаем, что одновременное обнаружение или потеря двух и более частот практически невозможно. Граф состояний системы показан на рис. 2.7.

увеличить изображение
Рис. 2.7. Граф состояний системы пеленгации
Граф соответствует процессу "гибели и размножения", полносвязный, число состояний системы, конечно, значит, установившийся режим, и предельные значения вероятностей в системе пеленгации существуют.
Пусть, к примеру, количество операторов 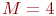 , а количество передатчиков противника
, а количество передатчиков противника 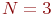 . В этом случае граф состояний имеет вид (рис. 2.8):
. В этом случае граф состояний имеет вид (рис. 2.8):
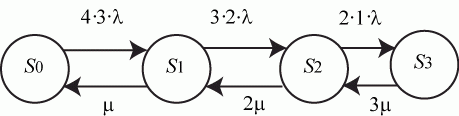
Рис. 2.8. Вариант графа состояний системы пеленгации
Для упрощения вычислений примем  . Тогда для этой схемы "гибели и размножения" по зависимостям (2.2) имеем:
. Тогда для этой схемы "гибели и размножения" по зависимостям (2.2) имеем:
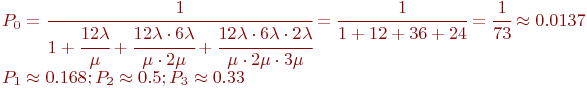
Окончательно:
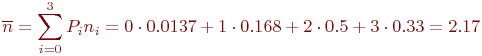
Таким образом, в условиях данного примера в среднем будут пеленговаться не менее двух передатчиков противника.
Непрерывный марковский процесс полностью определяется значениями плотностей вероятностей переходов 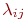 ,
,  Ранее был установлен их физический смысл как интенсивности потоков событий, переводящих систему из одного состояния в другое. Поток событий в однородных непрерывных марковских процессах характеризуется экспоненциальным законом распределения случайных интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
Ранее был установлен их физический смысл как интенсивности потоков событий, переводящих систему из одного состояния в другое. Поток событий в однородных непрерывных марковских процессах характеризуется экспоненциальным законом распределения случайных интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
Простейший поток обладает свойствами:
- стационарности,что означает независимость характеристик потока от времени;
- ординарности, что означает практическую невозможность появления двух и более событий одновременно;
- отсутствия последействия, об этом говорилось в начале темы.
2.4. Элементы СМО, краткая характеристика
При решении задач управления, в том числе и управления войсками, часто возникает ряд однотипных задач:
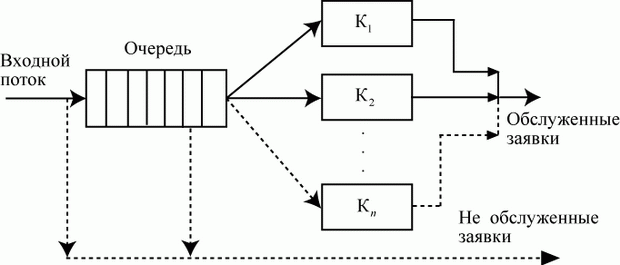 увеличить изображение Рис. 2.9. Система массового обслуживания
Элементами СМО являются:
увеличить изображение Рис. 2.9. Система массового обслуживания
Элементами СМО являются:
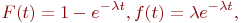 здесь
здесь 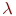 - интенсивность потока.
Название потока - пуассоновский - происходит от того, что для этого потока вероятность - интенсивность потока.
Название потока - пуассоновский - происходит от того, что для этого потока вероятность 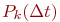 появления появления 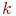 заявок за интервал заявок за интервал 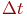 определяется законом Пуассона: определяется законом Пуассона:
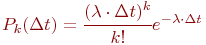 Поток такого типа, как отмечалось ранее, называют также простейшим. Именно такой поток предполагают проектировщики при разработке СМО. Вызвано это тремя причинами.
Во-первых,поток этого типа в теории массового обслуживания аналогичен нормальному закону распределения в теории вероятностей в том смысле, что к простейшему потоку приводит предельный переход для потока, являющегося суммой потоков с произвольными характеристиками при бесконечном увеличении слагаемых и уменьшении их интенсивности. То есть сумма произвольных независимых (без преобладания) потоков с интенсивностями
Поток такого типа, как отмечалось ранее, называют также простейшим. Именно такой поток предполагают проектировщики при разработке СМО. Вызвано это тремя причинами.
Во-первых,поток этого типа в теории массового обслуживания аналогичен нормальному закону распределения в теории вероятностей в том смысле, что к простейшему потоку приводит предельный переход для потока, являющегося суммой потоков с произвольными характеристиками при бесконечном увеличении слагаемых и уменьшении их интенсивности. То есть сумма произвольных независимых (без преобладания) потоков с интенсивностями 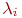 является простейшим потоком с интенсивностью является простейшим потоком с интенсивностью
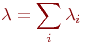 Во-вторых,если обслуживающие каналы (приборы) рассчитаны на простейший поток заявок, то обслуживание других типов потоков (с той же интенсивностью) будет обеспечено с не меньшей эффективностью.
В-третьих,именно такой поток определяет марковский процесс в системе и, следовательно, простоту аналитического анализа системы. При других потоках анализ функционирования СМО сложен.
Часто встречаются системы, у которых поток входных заявок зависит от количества заявок, находящихся в обслуживании. Такие СМО называют замкнутыми(иначе - разомкнутыми). Например, работа мастерской связи объединения может быть представлена моделью замкнутой СМО. Пусть эта мастерская предназначена для обслуживания радиостанций, которых в объединении
Во-вторых,если обслуживающие каналы (приборы) рассчитаны на простейший поток заявок, то обслуживание других типов потоков (с той же интенсивностью) будет обеспечено с не меньшей эффективностью.
В-третьих,именно такой поток определяет марковский процесс в системе и, следовательно, простоту аналитического анализа системы. При других потоках анализ функционирования СМО сложен.
Часто встречаются системы, у которых поток входных заявок зависит от количества заявок, находящихся в обслуживании. Такие СМО называют замкнутыми(иначе - разомкнутыми). Например, работа мастерской связи объединения может быть представлена моделью замкнутой СМО. Пусть эта мастерская предназначена для обслуживания радиостанций, которых в объединении 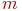 . Каждая из них имеет интенсивность отказов . Каждая из них имеет интенсивность отказов 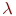 . Входной поток отказавшей аппаратуры будет иметь интенсивность . Входной поток отказавшей аппаратуры будет иметь интенсивность 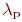 : :
 где
где 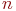 - количество радиостанций, уже находящихся в мастерской на ремонте.
Заявки могут иметь разные права на начало обслуживания. В этом случае говорят, что заявки неоднородные. Преимущества одних потоков заявок перед другими задаются шкалой приоритетов.
Важной характеристикой входного потока является коэффициент вариации: - количество радиостанций, уже находящихся в мастерской на ремонте.
Заявки могут иметь разные права на начало обслуживания. В этом случае говорят, что заявки неоднородные. Преимущества одних потоков заявок перед другими задаются шкалой приоритетов.
Важной характеристикой входного потока является коэффициент вариации:
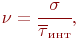 где
где  - математическое ожидание длины интервала; - математическое ожидание длины интервала;
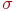 - среднеквадратическое отклонение случайной величины (длины интервала) - среднеквадратическое отклонение случайной величины (длины интервала)  .
Для простейшего потока .
Для простейшего потока 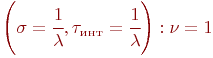 Для большинства реальных потоков
Для большинства реальных потоков 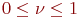 .
При .
При 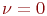 поток регулярный, детерминированный.
Коэффициент вариации - характеристика, отражающая степень неравномерности поступления заявок.
Каналы (приборы) обслуживания. В СМО могут быть один или несколько обслуживающих приборов (каналов). Согласно с этим СМО называют одноканальными или многоканальными.
МногоканальныеСМО могут состоять из однотипных или разнотипных приборов. Обслуживающими приборами могут быть: поток регулярный, детерминированный.
Коэффициент вариации - характеристика, отражающая степень неравномерности поступления заявок.
Каналы (приборы) обслуживания. В СМО могут быть один или несколько обслуживающих приборов (каналов). Согласно с этим СМО называют одноканальными или многоканальными.
МногоканальныеСМО могут состоять из однотипных или разнотипных приборов. Обслуживающими приборами могут быть:
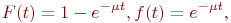 где
где 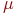 - интенсивность обслуживания, - интенсивность обслуживания, 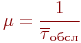 ; ;
 - математическое ожидание времени обслуживания.
То есть процесс обслуживания - марковский, а это, как теперь нам известно, дает существенные удобства в аналитическом математическом моделировании.
Кроме экспоненциального встречаются - математическое ожидание времени обслуживания.
То есть процесс обслуживания - марковский, а это, как теперь нам известно, дает существенные удобства в аналитическом математическом моделировании.
Кроме экспоненциального встречаются 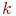 -распределение Эрланга, гиперэкспоненциальное, треугольное и некоторые другие. Это нас не должно смущать, так как показано, что значение критериев эффективности СМО мало зависят от вида закона распределения вероятностей времени обслуживания.
При исследовании СМО выпадает из рассмотрения сущность обслуживания, качество обслуживания.
Каналы могут быть абсолютно надежными, то есть не выходить из строя. Вернее, так может быть принято при исследовании. Каналы могут обладать конечной надежностью. В этом случае модель СМО значительно сложнее.
Очередь заявок. В силу случайного характера потоков заявок и обслуживания пришедшая заявка может застать канал (каналы) занятым обслуживанием предыдущей заявки. В этом случае она либо покинет СМО не обслуженной, либо останется в системе, ожидая начало своего обслуживания. В соответствии с этим различают: -распределение Эрланга, гиперэкспоненциальное, треугольное и некоторые другие. Это нас не должно смущать, так как показано, что значение критериев эффективности СМО мало зависят от вида закона распределения вероятностей времени обслуживания.
При исследовании СМО выпадает из рассмотрения сущность обслуживания, качество обслуживания.
Каналы могут быть абсолютно надежными, то есть не выходить из строя. Вернее, так может быть принято при исследовании. Каналы могут обладать конечной надежностью. В этом случае модель СМО значительно сложнее.
Очередь заявок. В силу случайного характера потоков заявок и обслуживания пришедшая заявка может застать канал (каналы) занятым обслуживанием предыдущей заявки. В этом случае она либо покинет СМО не обслуженной, либо останется в системе, ожидая начало своего обслуживания. В соответствии с этим различают:
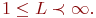 Исследователя обычно интересуют такие статистические характеристики, связанные с пребыванием заявок в очереди:
Исследователя обычно интересуют такие статистические характеристики, связанные с пребыванием заявок в очереди:
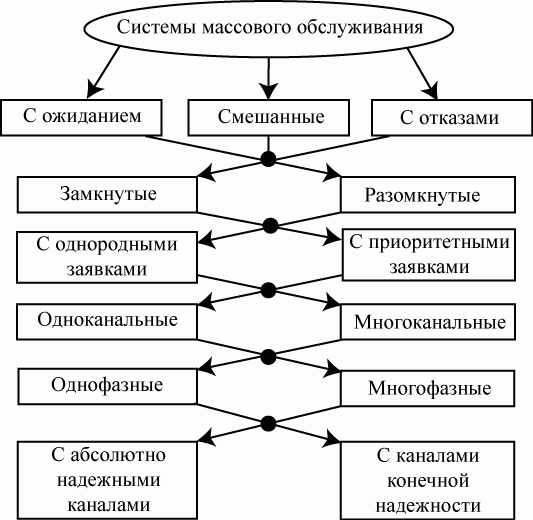 Рис. 2.10. Классификация СМО
Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом:
Рис. 2.10. Классификация СМО
Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом:
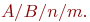
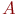 - входящий поток заявок: - входящий поток заявок: 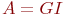 - рекуррентный поток; - рекуррентный поток; 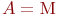 - простейший поток с показательным законом распределения вероятностей; - простейший поток с показательным законом распределения вероятностей; 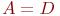 - регулярный или детерминированный поток (с постоянными интервалами между моментами поступления заявок). - регулярный или детерминированный поток (с постоянными интервалами между моментами поступления заявок).
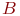 - случайная длительность обслуживания: - случайная длительность обслуживания: 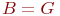 или или 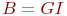 - рекуррентное обслуживание с одной и той же функцией распределения - рекуррентное обслуживание с одной и той же функцией распределения 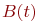 для разных каналов; для разных каналов; 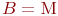 - показательное обслуживание; - показательное обслуживание; 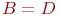 - регулярное обслуживание. - регулярное обслуживание.
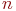 - количество обслуживающих каналов. Если - количество обслуживающих каналов. Если 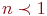 , то система называется многоканальной. , то система называется многоканальной.
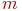 - количество мест для ожидания заявок в очереди. Если - количество мест для ожидания заявок в очереди. Если 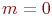 , то СМО с потерями (без ожидания); , то СМО с потерями (без ожидания); 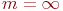 - система с неограниченным ожиданием; - система с неограниченным ожиданием;  - система с ограниченным числом мест для ожидания. - система с ограниченным числом мест для ожидания.
| |||||||||||||||

| |||||||||||||||

| |||||||||||||||
2.5.5. Одноканальная СМО с конечной надежностью
Построить граф состояний одноканальной СМО с очередью на три заявки и с конечной надежностью каналов обслуживания. При отказе канала обслуживания заявка, находившаяся на обслуживании, теряется. Процессы в системе - марковские.
Описание состояний СМО:
 - состояния исправной СМО; - состояния исправной СМО;
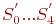 - состояния неисправной СМО.
Обозначения: - состояния неисправной СМО.
Обозначения:
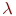 - интенсивность поступления заявок; - интенсивность поступления заявок;
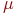 - интенсивность обработки заявки каналом; - интенсивность обработки заявки каналом;
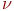 - интенсивность поломок канала; - интенсивность поломок канала;
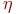 - интенсивность ремонта неисправного канала.
Граф состояний СМО с конечной надежностью каналов обслуживания приведен на рис. 2.14. - интенсивность ремонта неисправного канала.
Граф состояний СМО с конечной надежностью каналов обслуживания приведен на рис. 2.14.
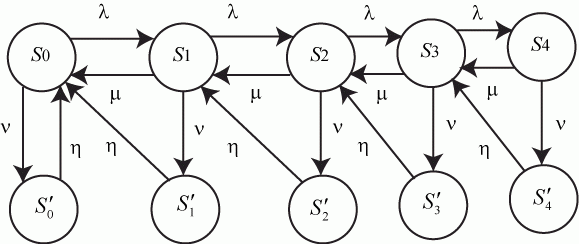 Рис. 2.14. Граф состояний СМО с конечной надежностью
Если в состоянии
Рис. 2.14. Граф состояний СМО с конечной надежностью
Если в состоянии 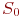 (канал свободен, в очереди заявок нет) система выйти из строя не может, то состояния (канал свободен, в очереди заявок нет) система выйти из строя не может, то состояния 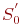 нет. Так как при отказе заявка, находившаяся на обслуживании, теряется, то после восстановления переход осуществляется к предыдущему состоянию, например, из состояния нет. Так как при отказе заявка, находившаяся на обслуживании, теряется, то после восстановления переход осуществляется к предыдущему состоянию, например, из состояния 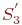 в состояние в состояние 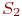 .
Эта модель не является моделью "гибели и размножения". Поэтому соответствующие вероятности находятся решением системы линейных алгебраических уравнений, полученных из уравнений Колмогорова для стационарного режима.
2.6. Метод динамики средних. Сущность и содержание метода
В многоэлементных системах часто целью моделирования является определение средних количеств элементов, находящихся в одинаковых состояниях.
Например, в задаче о пеленгации передатчиков противника командира интересует число запеленгированных передатчиков, а не вероятности пеленгации одного передатчика, двух, трех и т. д. Но чтобы определить среднее число их, надо знать вероятности всех возможных состояний .
Эта модель не является моделью "гибели и размножения". Поэтому соответствующие вероятности находятся решением системы линейных алгебраических уравнений, полученных из уравнений Колмогорова для стационарного режима.
2.6. Метод динамики средних. Сущность и содержание метода
В многоэлементных системах часто целью моделирования является определение средних количеств элементов, находящихся в одинаковых состояниях.
Например, в задаче о пеленгации передатчиков противника командира интересует число запеленгированных передатчиков, а не вероятности пеленгации одного передатчика, двух, трех и т. д. Но чтобы определить среднее число их, надо знать вероятности всех возможных состояний 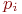 , так как , так как
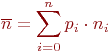 Но число состояний и, следовательно, число уравнений Колмогорова может оказаться настолько большим, что вызовет непреодолимые трудности при моделировании по схеме марковских процессов.
Например, в соединении имеется 100 радиостанций. Каждая из них может находиться в боевых условиях в пяти состояниях:
Но число состояний и, следовательно, число уравнений Колмогорова может оказаться настолько большим, что вызовет непреодолимые трудности при моделировании по схеме марковских процессов.
Например, в соединении имеется 100 радиостанций. Каждая из них может находиться в боевых условиях в пяти состояниях:
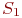 - исправна, работает, не обнаружена; - исправна, работает, не обнаружена;
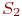 - исправна, работает, обнаружена; - исправна, работает, обнаружена;
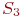 - работоспособна, но подавлена помехами; - работоспособна, но подавлена помехами;
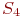 - обнаружена, поражена; - обнаружена, поражена;
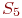 - находится в ремонте;
Для определения средних численностей каждого из этих состояний пришлось бы составить - находится в ремонте;
Для определения средних численностей каждого из этих состояний пришлось бы составить 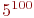 уравнений Колмогорова. Очевидно, такое моделирование не годится.
В исследовании операций есть метод, позволяющий успешно решать такие и аналогичные задачи. Этот метод называется метод динамики средних.
Метод динамики средних позволяет непосредственно определять математическое ожидание числа элементов сложной системы, находящихся в одинаковых состояниях.
Метод дает приближенные результаты. Но обладает замечательным свойством: чем больше система имеет элементов и состояний, тем точнее результат математического моделирования.
Для получения расчетных формул метода предположим, что имеем дело с системой, обладающей следующими признаками: уравнений Колмогорова. Очевидно, такое моделирование не годится.
В исследовании операций есть метод, позволяющий успешно решать такие и аналогичные задачи. Этот метод называется метод динамики средних.
Метод динамики средних позволяет непосредственно определять математическое ожидание числа элементов сложной системы, находящихся в одинаковых состояниях.
Метод дает приближенные результаты. Но обладает замечательным свойством: чем больше система имеет элементов и состояний, тем точнее результат математического моделирования.
Для получения расчетных формул метода предположим, что имеем дело с системой, обладающей следующими признаками:
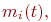 находящихся в одинаковых состояниях находящихся в одинаковых состояниях 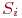 , и дисперсию , и дисперсию 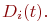 Схематично такая система может быть представлена так, как показано на рис. 2.15.
Система имеет
Схематично такая система может быть представлена так, как показано на рис. 2.15.
Система имеет 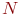 элементов, а каждый элемент имеет элементов, а каждый элемент имеет 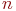 состояний. Численность состояний. Численность 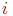 -го состояния на любой момент времени - величина случайная. Обозначим ее -го состояния на любой момент времени - величина случайная. Обозначим ее 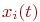 . Матожидание и дисперсия этой случайной величины: . Матожидание и дисперсия этой случайной величины:
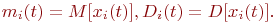 В дальнейшем для лучшей обозримости формул аргумент
В дальнейшем для лучшей обозримости формул аргумент 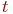 писать не будем: писать не будем:
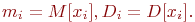
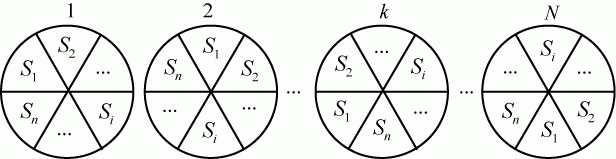 Рис. 2.15. Схематичное представление системы
Введем переменную
Рис. 2.15. Схематичное представление системы
Введем переменную 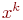 так что: так что:
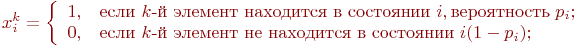 Отсюда следует, что случайная величина
Отсюда следует, что случайная величина 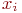 равна: равна:
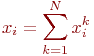 В силу однородности элементов и независимости состояний случайная величина
В силу однородности элементов и независимости состояний случайная величина 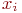 имеет биномиальное распределение (распределение Бернулли) с матожиданием и дисперсией соответственно: имеет биномиальное распределение (распределение Бернулли) с матожиданием и дисперсией соответственно:
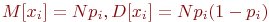 или окончательно
или окончательно
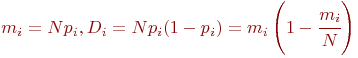 Равенство
Равенство 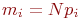 связывает вероятность связывает вероятность 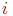 -го состояния элемента в произвольный момент времени с матожиданием численности этих состояний по всем элементам.
Определять значения -го состояния элемента в произвольный момент времени с матожиданием численности этих состояний по всем элементам.
Определять значения 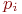 для одного элемента мы умеем. Для этого достаточно составить систему уравнений Колмогорова и решить ее.
Вспомним, что система уравнений Колмогорова для одного элемента содержит для одного элемента мы умеем. Для этого достаточно составить систему уравнений Колмогорова и решить ее.
Вспомним, что система уравнений Колмогорова для одного элемента содержит 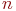 уравнений, а для всех уравнений, а для всех 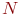 элементов - элементов - 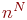 , то есть в , то есть в 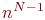 раз меньше. В этом и состоит выигрыш, который дает применение метода динамики средних.
Порядок моделирования с использованием метода динамики средних заключается в следующем. раз меньше. В этом и состоит выигрыш, который дает применение метода динамики средних.
Порядок моделирования с использованием метода динамики средних заключается в следующем.
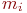 , об условиях существования установившихся значений , об условиях существования установившихся значений 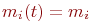 .
Полученные уравнения для .
Полученные уравнения для 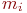 называют уже не уравнениями Колмогорова, а уравнениями динамики средних.Поскольку они получаются из уравнений Колмогорова путем умножения всех членов на постоянное число называют уже не уравнениями Колмогорова, а уравнениями динамики средних.Поскольку они получаются из уравнений Колмогорова путем умножения всех членов на постоянное число 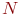 , то их можно писать сразу для средних численностей состояний , то их можно писать сразу для средних численностей состояний 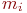 по образцу уравнений для вероятностей по образцу уравнений для вероятностей 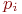 .
Рассмотрим на примере методику моделирования с использованием метода динамики средних.
Пример 2.8.В части имеются 100 средств связи (СС). СС выходят из строя с интенсивностью .
Рассмотрим на примере методику моделирования с использованием метода динамики средних.
Пример 2.8.В части имеются 100 средств связи (СС). СС выходят из строя с интенсивностью 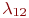 . При нахождении СС в неисправном состоянии проводится его диагностика, в результате чего оно может быть отправлено в ремонтное подразделение части (интенсивность отправки . При нахождении СС в неисправном состоянии проводится его диагностика, в результате чего оно может быть отправлено в ремонтное подразделение части (интенсивность отправки 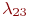 ), либо во внешнее ремонтное подразделение (интенсивность отправки ), либо во внешнее ремонтное подразделение (интенсивность отправки 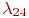 ), либо списано (интенсивность списания ), либо списано (интенсивность списания 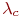 ). В ремонтном подразделении части СС ремонтируются с интенсивностью ). В ремонтном подразделении части СС ремонтируются с интенсивностью 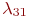 , а во внешнем ремонтном подразделении - с интенсивностью , а во внешнем ремонтном подразделении - с интенсивностью 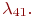 СС части пополняются с интенсивностью СС части пополняются с интенсивностью 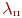 , в среднем равной интенсивности списания.
Требуется провести моделирование с целью определения средних численностей каждого состояния СС.
Решение , в среднем равной интенсивности списания.
Требуется провести моделирование с целью определения средних численностей каждого состояния СС.
Решение
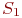 - СС исправно; - СС исправно;
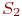 - СС неисправно, производится диагностика; - СС неисправно, производится диагностика;
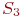 - СС находится на ремонте в ремонтном подразделении части; - СС находится на ремонте в ремонтном подразделении части;
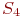 - СС находится на ремонте во внешнем ремонтном подразделении. - СС находится на ремонте во внешнем ремонтном подразделении.
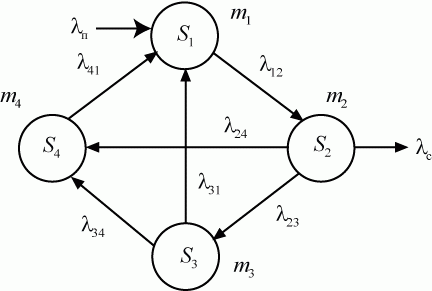 Рис. 2.16. Размеченный граф состояний системы ремонта
Рис. 2.16. Размеченный граф состояний системы ремонта
 Численности состояний являются функциями времени, т. е.
Численности состояний являются функциями времени, т. е. 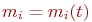 . В системе дифференциальных уравнений запись упрощена. Выражение для пополняющего члена написано из условия равенства в среднем пополнения и убыли . В системе дифференциальных уравнений запись упрощена. Выражение для пополняющего члена написано из условия равенства в среднем пополнения и убыли 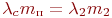 . Также мы не можем воспользоваться нормировочным условием . Также мы не можем воспользоваться нормировочным условием 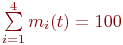 , так как в силу случайного характера списания и пополнения в некоторые моменты времени оно может не выполняться. Общее число СС в части при этом меняется со временем: , так как в силу случайного характера списания и пополнения в некоторые моменты времени оно может не выполняться. Общее число СС в части при этом меняется со временем:
Решить систему ДУ можно методом численного интегрирования, например, Рунге-Кутта, задав начальные значения численно-стей состояний для момента
считая интенсивности
Дисперсия вычисляется по формуле:
По дисперсии определяется среднеквадратическое отклонение численности состояний Метод динамики средних справедлив и для предельных значений численностей состояний. В данной задаче уравнения динамики средних - система линейных алгебраических уравнений:
Однако прежде чем переходить к этим уравнениям, нужно сначала убедиться, что стационарные значения |
Как показывает практика, метод динамики средних вполне приемлем и для немарковских процессов, то есть для произвольных распределений времен нахождения элементов в состояниях 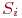 .
.
Хотя в этих случаях мы формально не имеем право написать уравнения динамики средних, однако массовость явления делает вид распределения не очень существенным. Следовательно, при моделировании не следует тратить время на проверку марковости процесса. Чем больше элементов в системе, чем она сложнее, тем точнее она моделируется методом динамики средних.
При большом числе элементов также становится не очень существенным требование однородности элементов.
Теперь попробуем разобраться с требованием, которое мы также ввели ранее - требование независимости элементов.
Применяя метод динамики средних, мы можем встретиться с очень серьезной трудностью. Дело в том, что интенсивности потоков событий, переводящих элементы из одного состояния в другое, могут зависеть от численности состояний. Например, в примере 2.6 интенсивность 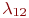 зависит от того, сколько в данный момент времени находится СС в состоянии
зависит от того, сколько в данный момент времени находится СС в состоянии 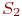 : СС может либо сразу ремонтироваться, либо ожидать очереди ввиду занятости рабочих мест. Численности состояний случайны, следовательно, интенсивности потоков событий тоже случайны и неизвестны. Точное решение в таких ситуациях невозможно, однако вполне приемлемое
: СС может либо сразу ремонтироваться, либо ожидать очереди ввиду занятости рабочих мест. Численности состояний случайны, следовательно, интенсивности потоков событий тоже случайны и неизвестны. Точное решение в таких ситуациях невозможно, однако вполне приемлемое
для практики решение находится с помощью допущения, которое называют "принцип квазирегулярности". Принцип квазирегулярности состоит в следующем: интенсивности 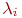 зависят не от мгновенных значений численности состояний
зависят не от мгновенных значений численности состояний 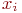 , а от их средних значений (математических ожиданий)
, а от их средних значений (математических ожиданий) 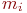 .
.
Погрешность от этого допущения при моделировании тем меньше, чем ближе к линейной зависимости  и чем больше общее количество элементов
и чем больше общее количество элементов 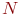 .
.
На практике проверено, что при  точность моделирования приемлема для инженерных "прикидок", если же функции
точность моделирования приемлема для инженерных "прикидок", если же функции  близки к линейным, то приемлемые результаты получаются и при
близки к линейным, то приемлемые результаты получаются и при 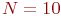 .
.
Пример 2.9. Каждый автомат, находящийся на вооружении в воинской части, может находиться в исправном состоянии или ремонтироваться в мастерской части. Если бы каждый неисправный автомат сразу попадал к свободному мастеру, то никаких очередей из автоматов, ожидающих ремонта, не было, и граф состояний автомата имел бы вид, приведенный на рис. 2.17.
Здесь:
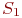 - автомат исправен;
- автомат исправен;
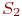 - автомат неисправен, ремонтируется;
- автомат неисправен, ремонтируется;
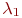 - интенсивность выхода автомата из строя;
- интенсивность выхода автомата из строя;
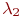 - интенсивность ремонта автомата одним мастером.
- интенсивность ремонта автомата одним мастером.
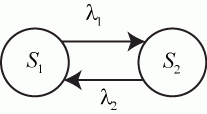
Рис. 2.17. Граф состояний автомата
В этом случае 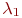 и
и 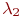 были бы постоянными величинами и, естественно, не зависели от численности состояний. Уравнения динамики средних имели бы вид:
были бы постоянными величинами и, естественно, не зависели от численности состояний. Уравнения динамики средних имели бы вид:
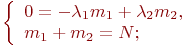
так как мы полагаем, что процессы наработки на отказ и ремонта - марковские и стационарный режим существует. 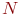 - общее число автоматов в части.
- общее число автоматов в части.
Уравнение для состояния 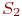 не пишем, так как оно линейно зависит от первого.
не пишем, так как оно линейно зависит от первого.
А теперь предположим, что в мастерской части два мастера и неисправные автоматы могут ожидать ремонта. В этом случае интенсивность переходов из неисправного состояние в исправное зависит от числа автоматов, находящихся в мастерской. Обозначим эту интенсивность 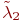 . Граф состояний имеет вид (рис. 2.18).
. Граф состояний имеет вид (рис. 2.18).
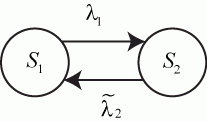
Рис. 2.18. Граф состояний автомата
Общую интенсивность ремонта мастерской обозначим 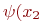 ). График ее показан на рис. 2.19а.
). График ее показан на рис. 2.19а.

Рис. 2.19. Графики \phi(x2) и \lambda 2
При 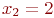 интенсивность
интенсивность 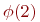 максимальна, так как работают оба мастера. При дальнейшем увеличении
максимальна, так как работают оба мастера. При дальнейшем увеличении 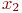 } интенсивность
} интенсивность 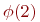
возрастать не может. Очевидно, интенсивность ремонта, приходящаяся на один автомат, находящийся в мастерской:
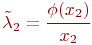
График зависимости 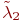 от
от 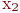 показан на рис. 2.19б.
показан на рис. 2.19б.
Применим принцип квазирегулярности, то есть будем считать, что 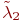 зависит не от случайных численностей
зависит не от случайных численностей 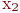 , а от среднего значения (матожидания)
, а от среднего значения (матожидания) 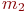 . Тогда:
. Тогда:
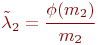
и уравнения динамики средних примут вид:
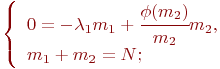
Зависимость  задана рис. 2.19б.
задана рис. 2.19б.
Пример 2.10. Вернемся к задаче о пеленгации передатчиков противника. Поскольку целью ее решения являлось определение среднего числа запеленгованных передатчиков, то возможно применение метода динамики средних. Обозначим:
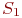 - состояние "передатчик запеленгован";
- состояние "передатчик запеленгован";
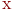 - случайная численность состояния
- случайная численность состояния 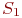 ;
;
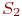 - состояние "передатчик потерян";
- состояние "передатчик потерян";
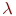 - интенсивность обнаружения частоты передатчика противника одним оператором;
- интенсивность обнаружения частоты передатчика противника одним оператором;
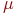 - интенсивность потерь слежения запеленгованного передатчика противника;
- интенсивность потерь слежения запеленгованного передатчика противника;
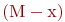 - текущее число операторов, ведущих поиск;
- текущее число операторов, ведущих поиск;
 - интенсивность обнаружения всеми операторами одного передатчика;
- интенсивность обнаружения всеми операторами одного передатчика;
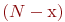 - число не захваченных частот передатчиков, находящихся в состоянии
- число не захваченных частот передатчиков, находящихся в состоянии 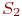 .
.
Граф состояний одного передатчика приведен на рис. 2.20. Заменим, в соответствии с принципом квазирегулярности, случайную численность обнаруженных передатчиков 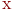 на среднее значение
на среднее значение 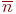 и, учитывая наличие стационарности, запишем уравнение динамики средних:
и, учитывая наличие стационарности, запишем уравнение динамики средних:
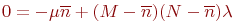
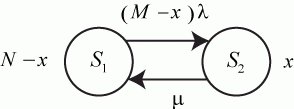
Рис. 2.20. Граф состояний передатчика
Уравнения динамики средних могут быть нелинейными и, следовательно, решение будет не единственным. В таких случаях берется то решение, которое не противоречит смыслу задачи.
Для упрощения расчетов положим 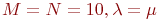 . В этом случае уравнение принимает вид:
. В этом случае уравнение принимает вид:
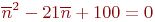
Его решение 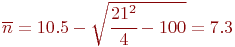 передатчика (знак плюс перед корнем отбрасываем, так как в этом случае корень будет равен 13,7, что бессмысленно). Решение этого примера с помощью уравнений Колмогорова дает ответ
передатчика (знак плюс перед корнем отбрасываем, так как в этом случае корень будет равен 13,7, что бессмысленно). Решение этого примера с помощью уравнений Колмогорова дает ответ 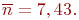 Расхождение в 2,5 % объясняется малочисленностью группировок
Расхождение в 2,5 % объясняется малочисленностью группировок 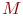 и
и 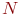 . Впрочем, полученный результат может быть вполне приемлемым.
. Впрочем, полученный результат может быть вполне приемлемым.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1340; Нарушение авторских прав?; Мы поможем в написании вашей работы!
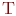 .
В зависимости от типа системы показателями исхода операции или эффективности системы массового обслуживания являются следующие.
Для СМО с отказами:
.
В зависимости от типа системы показателями исхода операции или эффективности системы массового обслуживания являются следующие.
Для СМО с отказами:
 )- среднее число заявок, обслуживаемое системой за время
)- среднее число заявок, обслуживаемое системой за время 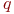 )- средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуженных заявок к среднему числу поступивших за время
)- средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуженных заявок к среднему числу поступивших за время 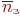 );
);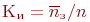 , где
, где 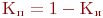 .
. );
);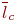 );
);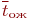 );
);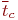 );
);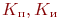 );
);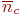 ,
, 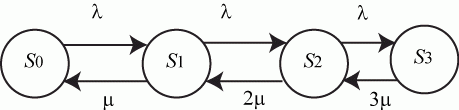 Рис. 2.11. Граф состояний трехканальной СМО с отказами
На графе:
Рис. 2.11. Граф состояний трехканальной СМО с отказами
На графе: 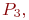 используя зависимости (2.2).
используя зависимости (2.2).
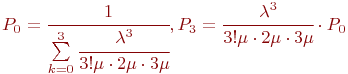 Пропускную способность этого поста автоинспекторов можно характеризовать относительной пропускной способностью:
Пропускную способность этого поста автоинспекторов можно характеризовать относительной пропускной способностью:
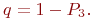 Пример 2.6. Для приема и обработки донесений от разведгруппы в разведотделе объединения назначена группа в составе трех офицеров. Ожидаемая интенсивность потока донесений - 15 донесений в час. Среднее время обработки одного донесения одним офицером -
Пример 2.6. Для приема и обработки донесений от разведгруппы в разведотделе объединения назначена группа в составе трех офицеров. Ожидаемая интенсивность потока донесений - 15 донесений в час. Среднее время обработки одного донесения одним офицером - 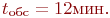 Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.
Определить, достаточно ли назначенной группы из трех офицеров для выполнения поставленной задачи.
Решение
Группа офицеров работает как СМО с отказами, состоящая из
трех каналов. Поток донесений с интенсивностью
Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.
Определить, достаточно ли назначенной группы из трех офицеров для выполнения поставленной задачи.
Решение
Группа офицеров работает как СМО с отказами, состоящая из
трех каналов. Поток донесений с интенсивностью 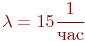 можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания
можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания 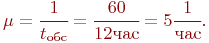 Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.
Описание состояний и граф состояний СМО будут аналогичны приведенным в примере 2.5.
Поскольку граф состояний - это схема "гибели и размножения", то для нее имеются готовые выражения для предельных вероятностей состояния:
Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.
Описание состояний и граф состояний СМО будут аналогичны приведенным в примере 2.5.
Поскольку граф состояний - это схема "гибели и размножения", то для нее имеются готовые выражения для предельных вероятностей состояния:
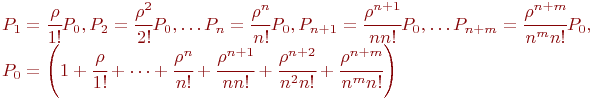 Отношение
Отношение 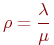 называют приведенной интенсивностью потока заявок.Физический смысл ее следующий: величина
называют приведенной интенсивностью потока заявок.Физический смысл ее следующий: величина 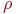 представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
В примере
представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
В примере 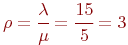 .
В рассматриваемой СМО отказ наступает при занятости всех трех каналов, то есть
.
В рассматриваемой СМО отказ наступает при занятости всех трех каналов, то есть 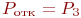 . Тогда:
. Тогда:
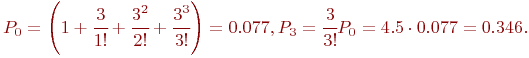 Так как вероятность отказа в обработке донесений составляет более 34 % (
Так как вероятность отказа в обработке донесений составляет более 34 % ( ), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем
), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем 
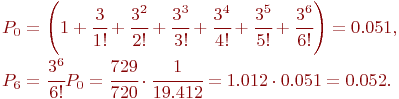 Теперь
Теперь 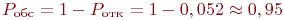 .
Таким образом, только группа из шести офицеров сможет обрабатывать поступающие донесения с вероятностью 95 %.
2.5.2. Многоканальная СМО с ожиданием
Пример 2.7. На участке форсирования реки имеются 15 однотипных переправочных средств. Поток поступления техники на переправу в среднем составляет 1 ед./мин, среднее время переправы одной единицы техники - 10 мин (с учетом возвращения назад переправочного средства).
Оценить основные характеристики переправы, в том числе вероятность в немедленной переправе сразу по прибытии единицы техники.
Решение
.
Таким образом, только группа из шести офицеров сможет обрабатывать поступающие донесения с вероятностью 95 %.
2.5.2. Многоканальная СМО с ожиданием
Пример 2.7. На участке форсирования реки имеются 15 однотипных переправочных средств. Поток поступления техники на переправу в среднем составляет 1 ед./мин, среднее время переправы одной единицы техники - 10 мин (с учетом возвращения назад переправочного средства).
Оценить основные характеристики переправы, в том числе вероятность в немедленной переправе сразу по прибытии единицы техники.
Решение
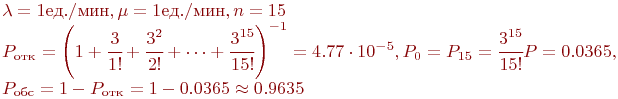 Абсолютная пропускная способность
Абсолютная пропускная способность 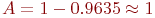 , т. е. все, что подходит к переправе, тут же практически переправляется.
Среднее число работающих переправочных средств:
, т. е. все, что подходит к переправе, тут же практически переправляется.
Среднее число работающих переправочных средств:
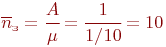 Коэффициенты использования и простоя переправы:
Коэффициенты использования и простоя переправы:
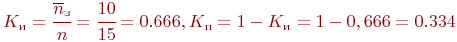 Для решения примера была также разработана программа. Интервалы времени поступления техники на переправу, время переправы приняты распределенными по экспоненциальному закону.
Коэффициенты использования переправы после 50 прогонов практически совпадают:
Для решения примера была также разработана программа. Интервалы времени поступления техники на переправу, время переправы приняты распределенными по экспоненциальному закону.
Коэффициенты использования переправы после 50 прогонов практически совпадают:  .
Максимальная длина очереди 15 ед., среднее время пребывания в очереди около 10 мин.
Если взять число переправочных средств 10, то коэффициент использования близок к 1 (
.
Максимальная длина очереди 15 ед., среднее время пребывания в очереди около 10 мин.
Если взять число переправочных средств 10, то коэффициент использования близок к 1 (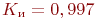 ), максимальная длина очереди - 43 единицы техники.
2.5.3. Одноканальная СМО с ограниченной очередью
Если в очереди
), максимальная длина очереди - 43 единицы техники.
2.5.3. Одноканальная СМО с ограниченной очередью
Если в очереди  состояний:
состояний:
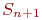 - в системе обслуживается одна заявка и
- в системе обслуживается одна заявка и  Рис. 2.12. Граф состояний одноканальной СМО с ограниченной очередью
2.5.4. Одноканальная замкнутая СМО
Опишем состояния одноканальной замкнутой СМО.
Рис. 2.12. Граф состояний одноканальной СМО с ограниченной очередью
2.5.4. Одноканальная замкнутая СМО
Опишем состояния одноканальной замкнутой СМО.
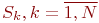 - на обслуживании находится
- на обслуживании находится 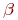 - интенсивность требований на обслуживание от одной заявки.
Граф состояний одноканальной замкнутой СМО приведен на рис. 2.13. Модель данной СМО также представляет "схему гибели и размножения".
- интенсивность требований на обслуживание от одной заявки.
Граф состояний одноканальной замкнутой СМО приведен на рис. 2.13. Модель данной СМО также представляет "схему гибели и размножения".
 увеличить изображение Рис. 2.13. Граф состояний одноканальной замкнутой СМО
Однако не менее часто модель СМО не сводится к схеме "гибели и размножения". Например, в СМО с конечной надежностью каналов обслуживания.
увеличить изображение Рис. 2.13. Граф состояний одноканальной замкнутой СМО
Однако не менее часто модель СМО не сводится к схеме "гибели и размножения". Например, в СМО с конечной надежностью каналов обслуживания.


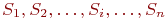 средние численности состояний
средние численности состояний 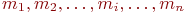 , полученные умножением
, полученные умножением 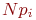 .
.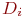 и средних квадратических отклонений
и средних квадратических отклонений  .
.
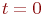 :
: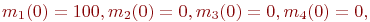
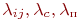 известными.
известными.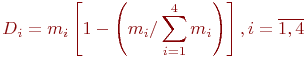
 .
.