Знакочередующиеся ряды. Определение. Числовой ряд, у которого два соседних члена имеют противоположные знаки, называется знакочередующимся рядом

Определение. Числовой ряд, у которого два соседних члена имеют противоположные знаки, называется знакочередующимся рядом.

Такой ряд можно представить в виде

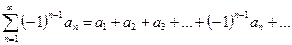(1)

Для знакочередующихся рядов имеется достаточный признак, часто используемый на практике

Теорема. (Признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине и предел общего члена равен нулю, то ряд (1) сходится.

Доказательство. Из условия теоремы следует

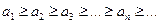(2)

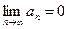(3)

Рассмотрим подпоследовательность частичных сумм с четным числом слагаемых

.

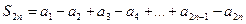Представим эту сумму в виде

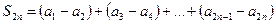. (4)

(Эта частичная сумма содержит конечное число слагаемых и, следовательно, можно группировать члены). В выражении (4) каждая скобка неотрицательная (в силу условий (2)), поэтому последовательность частичных сумм с четными номерами – неубывающая.

Эту же подпоследовательность можно представить по-другому.

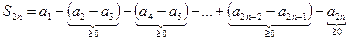
Из последнего выражения следует, что

.

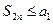Мы получили, что неубывающая подпоследовательность ограничена сверху, следовательно, она имеет предел. Введем обозначение

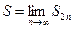. (5)

Теперь рассмотрим подпоследовательность частичных сумм ряда (1) с нечетным числом слагаемых

.

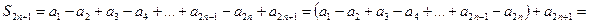
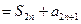Тогда

. (6)

Мы получили, что две подпоследовательности (с четным и нечетным числом слагаемых) последовательности частичных сумм ряда (1) сходятся к одному числу S, следовательно, 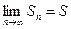, что означает, что ряд сходится.

Следствие 1. Если знакочередующийся ряд (1) удовлетворяет условиям теоремы Лейбница, то сумма этого ряда удовлетворяет условиям:

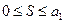
В процессе доказательства теоремы Лейбница были получены оценки

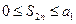
Перейдем в этом двойном неравенстве к пределу, с учетом соотношения (5), получим

,

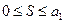что и требовалось доказать.

Следствие 2. Если знакочередующийся ряд (1) удовлетворяет условиям теоремы Лейбница, то абсолютная величина суммы любого остатка не превосходит первого отброшенного члена, т.е.

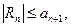(7)

где .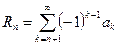

Доказательство. Рассмотрим остаток ряда (1) после номера 2n

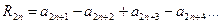
Согласно следствию 1

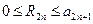. (8)

Теперь рассмотрим остаток ряда (1) после номера 2n-1

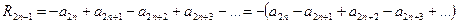
Тогда из следствия 1 получим

. (9)

Анализируя неравенства (8) и (9) приходим к выводу о справедливости неравенства (7).

Пример. Исследовать на сходимость ряд .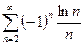

1) Ряд знакочередующийся;

2) Члены ряда убывают по абсолютной величине;

3) 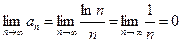. (для раскрытия неопределенности применили правило Лопиталя).

Таким образом, исследуемый ряд сходится по признаку Лейбница.

Дата добавления: 2014-01-11