Подільність многочленів

а) Ділення з остачею

Для розгляду теорії подільності многочленів від однієї змінної цілісне кільце R, якому належать усі коефіцієнти многочленів, потрібно замінити полем Р, для того, щоб для довільного елемента існував обернений елемент 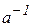, або щоб разом із довільними двома елементами 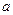, поля Р до цього ж поля належала і їх частка 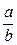. Цілісне кільце многочленів від однієї змінної з коефіцієнтами із поля Р позначають тепер P[x].

Два різні многочлени із P[x], як правило, не діляться один на одного. Однак для P[x] можна побудувати теорію подільності, аналогічну теорії подільності цілих чисел, якщо операцію ділення многочленів в P[x] замінити більш загальною операцією ділення з остачею.

Вважається, що многочлен ділиться з остачею на многочлен 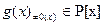, якщо в P[x] існують такі многочлени s(x) та r(x), що 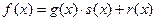, причому або r(x)=0, або deg r<deg g.

Теорема (про ділення з остачею).

Довільний многочлен f(x) з кільця P[x] однозначно ділиться з остачею на будь-який ненульовий многочлен з цього кільця.

Доведення.

Встановимо можливість ділення з остачею. Нехай

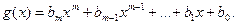
Якщо f(x)=0, то s(x)=0 і r(x)=0.

Якщо n=deg f<deg g=m, то s(x)=0 і r(x)=f(x).

Нехай n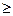m. Виконаємо доведення методом індукції за n.

При n=0 отримаємо m=0, f(x)=a₀, g(x)=b₀≠0, тому s(x)=, r(x)=0. Ясно, що s(x)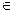P[x], бо P (ось де потрібна була заміна R на Р, здійснена на початку параграфа).

Припустимо, що теорема вірна для всіх многочленів f(x) степеня, меншого за n, і доведемо її для многочленів степеня n.

Розглянемо многочлен р(х)=f(x)–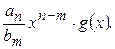 Cтарші члени обох многочленів справа є рівними а_nхⁿ, тобто взаємно знищаться. Тому deg p(x) < n і, за припущенням індукції, p(x) ділиться з остачею на g(x):

p(x)=g(x)·s₁(x)+r₁(x), де s₁(x),r₁(x) 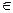P[x], r₁(x)=0 або deg r₁<deg g.

Звідси

f(x) - 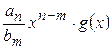= g(x)·s₁(x)+r₁(x), тобто

f(x)=g(x)·s(x)+r(x),

де r(x)=r₁(x)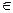P[x], s(x)=s₁(x),

причому r(x)=0 або deg r<deg g.

Можливість ділення f(x) на g(x) з остачею доведена.

Покажемо єдиність частки s(x) і остачі r(x). Припустимо, що можливі два варіанти:

f(x)=g(x)∙s(x)+r(x), deg r<deg g;

f(x)=g(x)∙s^*(x)+r^*(x), deg r^*<deg g.

Віднімемо рівності: g(x)[s(x) – s^*(x)]=r^*(x) – r(x).

За умовою g(x)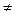0. Якщо б r(x)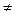r^*(x), то й s(x)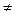s^*(x). Але тоді отримується суперечність, оскільки степінь правої частини менший степеня лівої частини. Отже, r(x)=r^*(x). Але тоді і s(x)=s^*(x). Таким чином, частка і остача єдині.▲

Наслідок. Кільце P[x] многочленів над полем Р є евклідовим.

На практиці ділення многочленів здійснюють відомим способом „ ділення кутом ”, в основі якого лежить метод, використаний при доведенні теореми про ділення з остачею.

Оскільки частка s(x) і остача r(x) визначаються однозначно, то для їх знаходження можна користуватися і методом невизначених коефіцієнтів, який ґрунтується на прирівнюванні коефіцієнтів при однакових степенях x в лівій і правій частині рівності f(x)=g(x)∙s(x)+r(x), де s(x) шукають у вигляді многочлена із невизначеними коефіцієнтами степеня n–m, а r(x) – степеня m-1.

Приклад.

Поділити f(x) на g(x) і знайти s(x) та r(x):

f(x)=x⁴-2x³+x-1, g(x)=x²-2.

1) Ділення кутом:

_ x^4–2x^3 +x –1	x^2–2
x^4 –2x^2	x^2–2x+2
_–2x^3+2x^2
–2x^3 +4x
		_2x^2–3x 2x^2 –4
	–3x+3

Отже, s(x)=x²–2x+2, r(x)= –3x+3.

2) Ділення методом невизначених коефіцієнтів:

x⁴–2x³+x–1=(x²–2)(A₂x²+A₁x+A₀)+(B₁x+B₀)

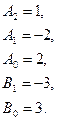
Отже, s(x)=x²–2x+2, r(x)= –3x+3.

б) Ділення многочлена на лінійний двочлен

Розглянемо важливий випадок ділення многочлена f(x) на лінійний двочлен x–α. Скористаємось методом невизначених коефіцієнтів.

a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀=(x–α)(A_n-1x^n-1+A_n-2x^n-2+…+A₁x+A₀)+r.

Тут r = const, оскільки deg r(x)=m–1=1–1=0.

Прирівнявши коефіцієнти в обох частинах, отримаємо:

a_n=A_n-1 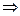A_n-1=a_n,

a_n-1=A_n-2-αA_n-1 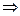A_n-2=a_n-1+αA_n-1,

- - - - - - - - - - - - - - - - - - - - - - - - - - - -

a₁=A₀-αA₁ 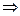A₀=a₁+αA₁,

a₀=r-αA₀ 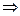r=a₀+αA₀.

Із отриманих формул випливає, що поділити многочлен на лінійний двочлен можна за певною схемою, яка називається схемою Горнера.

	a n	a n-1	a n-2	a n-3	…	a 1	a 0
α	a n   An-1	α An-1+ + a n-1     An-2	α An-2+ + a n-2     An-3	α An-3+ + a n-3     An-4		α A1+ + a 1     A1	α A0+ + a 0     A0

			-3		-2
			-2	-1	-3	-2
				-1	-4

Отже, s(x)=x⁴+x³-2x²-x-3, r= -2.

Теорема ( Безу). Для довільного елемента α поля Р остача при діленні

многочлена f(x)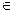P[x] на x-α дорівнює f(α).

Дійсно, згідно формули ділення з остачею f(x)=(x-α)s(x)+r. Підставимо x=α. Отримаємо f(α)=r, що й треба довести.▲

За допомогою багаторазового ділення многочлена f(x) на лінійний двочлен x-α з допомогою схеми Горнера можна дістати розклад многочлена f(x) за степенями двочлена x-α, який часто використовується в алгебрі та математичному аналізі.

f(x)=(x-α)f₁(x)+r₀,

f₁(x)=(x-α)f₂(x)+r₁,

f₂(x)=(x-α)f₃(x)+r₂,

- - - - - - - - - - - - -

f_n-1(x)=(x-α)f_n(x)+r_n-1.

Ясно, що f_n(x) є многочленом нульового степеня. Позначимо f_n(x)=r_n. Виключивши послідовно всі f_i(x), i=1, 2, …, n-1, отримаємо

f(x)=r_n(x-α)ⁿ+r_n-1(x-α)^n-1+…+r₁(x-α)+r₀.

Таким чином, отримаємо подання многочлена f(x) як многочлена від змінної y=x-α.

Приклад.

Знайти розклад многочлена f(x)=x⁵-3x³+x²-2x+1 за степенями двочлена x-1.

f(x)=(x-1)⁵+5(x-1)⁴+7(x-1)³+2(x-1)²-4(x-1)-2.

в) Подільність многочленів

Важливим для розгляду є випадок ділення многочленів “без остачі”, або, інакше, “націло”. Тоді говорять, що f(x) ділиться на g(x). Позначають: f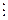(x)g(x).

Дата добавления: 2014-01-11