
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Найменше спільне кратне
|
|
|
|
Найменшим спільним кратним (НСК) многочленів f(x) та g(x) називається спільне кратне f(x) і g(x), на яке ділиться довільне інше спільне кратне цих многочленів. Позначається [f, g].
Теорема. Для довільних ненульових многочленів f(x), g(x) НСК існує і
визначається з точністю до сталого множника.
Доведення. Для доведення розглянемо многочлен 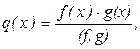 який, очевидно, є спільним кратним f(x) та g(x), оскільки ділиться на кожний з них. Нехай s(x) –довільне інше спільне кратне многочленів f(x) і g(x). Тоді
який, очевидно, є спільним кратним f(x) та g(x), оскільки ділиться на кожний з них. Нехай s(x) –довільне інше спільне кратне многочленів f(x) і g(x). Тоді  і
і 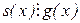 , звідки s(x)=s1(x)·f(x), а також
, звідки s(x)=s1(x)·f(x), а також 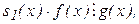 тобто
тобто
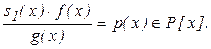
Замінимо f(x)=(f, g)·f1(x), g(x)=(f, g)·g1(x), де (f1, g1)=1. Звідси
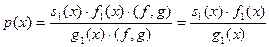 .
.
Із (f1, g1)=1 випливає, що 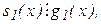 тобто s1(x)=g1(x)·t(x), звідки
тобто s1(x)=g1(x)·t(x), звідки 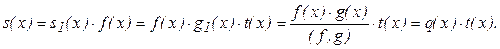 Отже,
Отже, 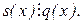
Це означає, що q(x) – найменше спільне кратне многочленів f(x) та g(x).
Якщо q1(x) – інше НСК, то 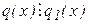 і
і 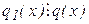 , тобто ql(x) та q(x) відрізняються тільки сталим множником.▲
, тобто ql(x) та q(x) відрізняються тільки сталим множником.▲
г) Звідність многочленів

Многочлен f(х)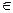 Р[x] називається незвідним у полі Р, якщо він не є константою і не має дільників, відмінних від константи та асоційованих з ним многочленів (аналог простого числа). В іншому випадку многочлен називають звідним (аналог складеного числа). Поняття звідності є відносним і залежить від поля Р, над яким розглядається многочлен.
Р[x] називається незвідним у полі Р, якщо він не є константою і не має дільників, відмінних від константи та асоційованих з ним многочленів (аналог простого числа). В іншому випадку многочлен називають звідним (аналог складеного числа). Поняття звідності є відносним і залежить від поля Р, над яким розглядається многочлен.
Приклад.
Многочлен f(х)=x 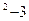 незвідний у полі Q, але звідний у полі R:
незвідний у полі Q, але звідний у полі R:
f(x)= (x-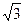 )(x+
)(x+ 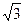 );
);
многочлен f(x)= x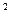 +3 незвідний в полях Q, R, але звідний у полі С:
+3 незвідний в полях Q, R, але звідний у полі С:
f(x)= (x-i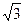 )(x+i
)(x+i 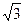 ).
).
Якщо многочлен f(х) незвідний у полі Р, то він вже є добутком незвідних в даному полі многочленів (один співмножник). Якщо многочлен f(х) звідний у полі Р, то, розклавши його і всі його співмножники в добуток незвідних многочленів у даному полі, отримаємо зображення многочлена, яке називають розкладом многочлена f(х) на незвідні множники:
f(x)=р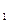 (х)р
(х)р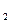 (х)...р
(х)...р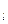 (х), де р
(х), де р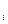 (х) – незвідні в полі Р, і =1,2,..., l.
(х) – незвідні в полі Р, і =1,2,..., l.
|
|
|
Звідси випливає ще один запис многочлена f(x):
f(x)=[p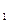 (x)]
(x)]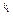 [p
[p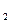 (x)]
(x)]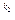 …[p
…[p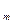 (x)]
(x)]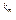 ,
,
де р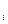 (х) – попарно різні (неасоційовані) многочлени, незвідні в полі Р.
(х) – попарно різні (неасоційовані) многочлени, незвідні в полі Р.
Таке зображення називають канонічним розкладом многочлена f(x) в полі Р.
д) Корені многочленів
Коренем многочлена f(x)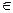 Р[x] називається елемент
Р[x] називається елемент 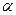 будь-якого розширення
будь-якого розширення 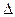 поля Р такий, що f (
поля Р такий, що f (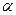 ) = 0.
) = 0.
Теорема . Елемент 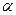 Є Р є коренем многочлена f(x)
Є Р є коренем многочлена f(x)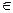 Р[x] тоді і тільки тоді,
Р[x] тоді і тільки тоді,
коли многочлен f(х) ділиться на х-α.
Доведення. За теоремою Безу f(х)=(х-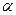 )f
)f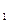 (x)+ f(
(x)+ f(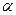 ). Звідси, f(х) ділиться на х-
). Звідси, f(х) ділиться на х-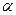 тоді і тільки тоді, коли f(
тоді і тільки тоді, коли f(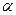 ) =0, тобто коли
) =0, тобто коли 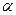 – корінь f(х). ▲
– корінь f(х). ▲ 
Інше (рівносильне при 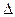 =Р) означення кореня.
=Р) означення кореня.
Коренем многочлена f(х)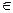 Р[x] називається такий елемент α
Р[x] називається такий елемент α 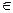 Р, для якого f(х)
Р, для якого f(х)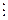 х-α.
х-α.
Елемент α 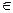 Р називається к- кратним коренем многочлена f(х)
Р називається к- кратним коренем многочлена f(х)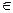 Р[x], якщо f(х) ділиться на (х-α)
Р[x], якщо f(х) ділиться на (х-α)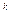 , але не ділиться на (х-α)
, але не ділиться на (х-α)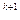 .
.
Кількість усіх можливих коренів многочлена f(х) над полем Р не перевищує степеня многочлена.
На питання, чи кожен многочлен ненульового степеня має хоча б один корінь, відповідь дає твердження, відоме під назвою теореми Кронекера:
Якщо f(х)-довільний многочлен ненульового степеня над полем Р, то існує розширення К поля Р, в якому є корінь f(х).
Наслідком із цього твердження є наступне:
Для довільного многочлена f(х)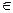 P[x] ненульового степеня існує таке розширення L поля Р, в якому f(х) розкладається на лінійні множники. Тобто, якщо
P[x] ненульового степеня існує таке розширення L поля Р, в якому f(х) розкладається на лінійні множники. Тобто, якщо  ,
,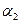 ,...,
,...,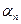
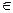 L є коренями многочлена f(х), то
L є коренями многочлена f(х), то
f(x)=a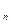 (x-
(x-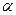
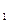 )(x--
)(x--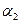 )…(x-
)…(x-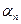 ),
),
де а 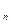 -старший коефіцієнт f(х).
-старший коефіцієнт f(х).
Поле L, в якому многочлен f(x) розкладається на лінійні множники, називається полем розкладу цього многочлена.
Приклад.
Знайти поле розкладу для многочлена f(x)=x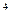 - 4.
- 4.
x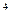 - 4=(x
- 4=(x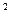 - 2)(x
- 2)(x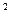 + 2)=(x -
+ 2)=(x -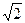 )(x+
)(x+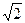 )(x-i
)(x-i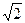 )(x+i
)(x+i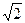 ).
).
Оскільки корені -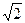 ,
,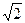 , -і
, -і 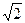 , і
, і 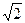 належать полю С, то поле С і є полем розкладу многочлена f(x)=x
належать полю С, то поле С і є полем розкладу многочлена f(x)=x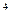 - 4.
- 4.
Поле Р називається алгебраїчно замкнутим, якщо воно є полем розкладу для довільного многочлена f(х)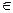 P[x] ненульового степеня, тобто якщо всі корені будь-якого многочлена f(х)
P[x] ненульового степеня, тобто якщо всі корені будь-якого многочлена f(х)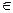 P[x] належить цьому ж полю.
P[x] належить цьому ж полю.
|
|
|
Поле С комплексних чисел є прикладом алгебраїчно замкнутого поля.
Теорема Вієта. Якщо  ,
, 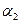 , ...,
, ..., 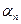 - корені многочлена
- корені многочлена
f(х)=а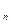 х
х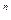 +а
+а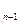 х
х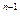 +...+а
+...+а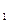 х+а
х+а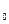
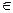 P[x], то
P[x], то
 +
+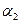 +...+
+...+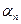 = -
= - 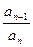 ,
,

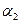 +
+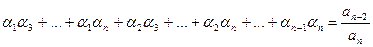 ,
,
………………………………………………………….
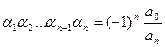 .
.
Доведення цього твердження здійснюється прирівнюванням коефіцієнтів при однакових степенях х в обох частинах.
Теорема 1. Якщо незвідний в полі Р характеристики 0 многочлен q(x) є
множником кратності k>1 многочлена f(x), то він є множником
кратності k-1 для похідної f¢(х).
Доведення. Якщо q(x) - множник кратності k многочлена f(х), то
f(x)=[q(x)]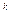 ·
·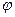 (x), де φ(x)
(x), де φ(x) 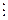 q(x).
q(x).
Тоді
f¢(x)=k[q(x)]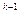 ·q¢(x)·
·q¢(x)·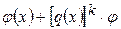 ¢(x)=[q(x)]k-1·[k·q¢(x)·
¢(x)=[q(x)]k-1·[k·q¢(x)· ¢(x)].
¢(x)].
Видно, що 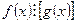
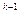 .
.
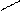 Залишилось показати, що вираз в других квадратних дужках не ділиться на
Залишилось показати, що вираз в других квадратних дужках не ділиться на 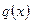 . Перший доданок на
. Перший доданок на 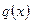 не ділиться, оскільки
не ділиться, оскільки 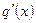 має нижчий степінь, ніж
має нижчий степінь, ніж 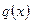 , а φ(x)
, а φ(x) 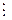 q(x) за умовою. Другий доданок ділиться на
q(x) за умовою. Другий доданок ділиться на 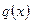 . Тоді сума
. Тоді сума
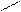 цих доданків на
цих доданків на 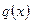 не ділиться. Отже,
не ділиться. Отже, 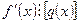
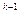 , тобто
, тобто 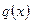 - множник
- множник 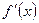 кратності k-1. ▲
кратності k-1. ▲
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 981; Нарушение авторских прав?; Мы поможем в написании вашей работы!