Многочлени над числовими полями

а)Многочлени над полем С

Теорема 1. Кожний многочлен степеня вищого одиниці є звідним в полі С.

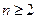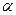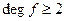Доведення. Якщо - многочлен степеня , то існує хоча б один корінь цього многочлена і, за наслідком з теореми Безу, , тобто . Оскільки , то 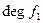>0, отже, звідний в полі С.▲

Наслідок 1. Для того, щоб многочлен був незвідним у полі С, необхідно і

достатньо, щоб його степінь дорівнював одиниці.

Наслідок 2. Кожний многочлен над полем С єдиним способом розкладається

на лінійні множники і цьому полі:,

де , , 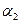…, 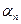- корені, 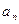- старший коефіцієнт многочлена .

Якщо в розкладі існують кратні множники, то, де ,,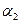…, - різні корені многочлена , ,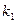,…, - відповідно їх кратності.

б) Многочлени над полем R

Теорема 2. Якщо комплексне число 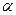є коренем многочлена над полем R,

то спряжене число теж є коренем цього многочлена.

Доведення. Обчислимо 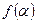і відокремимо дійсну та уявну частини:

.

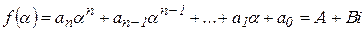Оскільки корінь , то , звідки , .

Обчислимо тепер . Оскільки 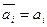, як дійсні числа, то

(бо ). Отже, 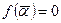, тобто - корінь .▲

Обидва корені 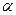та многочлена мають, зрозуміло, однакову кратність.

Теорема 3. Кожний многочлен над полем R, степінь якого перевищує 2, є

звідним у цьому полі.

Доведення. Нехай корінь многочлена над полем R степеня n >2.

Якщо R, то

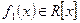, де і ,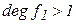

тобто звідний в полі R.

Якщ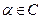о , то 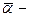теж корінь i

,

де і 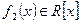, причому , тобто - звідний в R.

Із викладеного вище випливає наступне твердження:

кожний многочлен f(x) над полем R має єдиний розклад на незвідні множники в цьому полі:

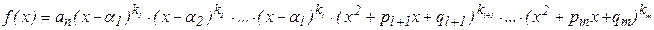
в) Многочлени над полем Q

Основна відмінність многочленів над полем Q від многочленів над полями R та С полягає в тому, що над полем Q існують многочлени як завгодно високого степеня, незвідні в полі Q, тоді як в кільці R[x] звідним є довільний многочлен степеня вищого 2, а в кільці С[x] – степеня вищого 1.

Ясно, що будь-яке алгебраїчне рівняння з раціональними коефіцієнтами множенням на спільний знаменник усіх коефіцієнтів можна звести до рівняння з цілими коефіцієнтами.

Терема Ейзенштейна (критерій незвідності).

Якщо в многочлені з цілими коефіцієнтами 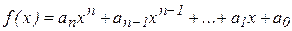коефіцієнти 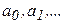,діляться на деяке просте число , причому не ділиться на , а старший коефіцієнт 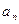не ділиться на , то многочлен незвідний у полі Q.

Доведення. Досить показати, що при заданих умовах не може бути добутком двох многочленів ненульового степеня з цілими коефіцієнтами. Припустимо супротивне, тобто, що .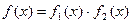

Тут r+s = n. Нехай .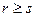

Тоді

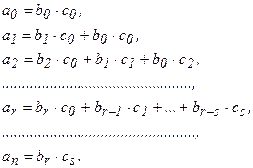
Оскільки , тобто , ділиться на , але не ділиться на , то на може ділитися лише одне з чисел: 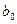або . Нехай 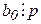, тоді . З другої рівності випливає, що (бо 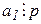за умовою, а с₀ 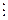р). Тоді з третьої рівності . Так можна показати, що всі коефіцієнти 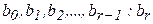діляться на . Але це неможливо, бо тоді й 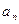ділилось б на (із останньої рівності), що суперечить умові теореми.

Отже, - незвідний в полі Q ▲.

Таким чином, у кільці многочленів над полем Q є многочлени довільного степеня, незвідні в полі Q.

Дата добавления: 2014-01-11