Многочлени від багатьох змінних

а) Загальні відомості

Кільцем многочленів R [ x₁, x₂, …, x_n-1, x_n ] від n змінних x₁, x₂, …, x_n-1, x_n над цілісним кільцем R називається кільце многочленів від змінної x_n над кільцем R [ x₁, x₂, …, x_n-1 ]:

R [ x₁, x₂, …, x_n-1, x_n ] =R [ x₁, x₂, …, x_n-1 ][ x_n ]. (3.1)

Це означення має індуктивний характер. При n =1 воно зводиться до означення кільця многочленів від однієї змінної x₁ над цілісним кільцем R. Якщо ж вже введено означення кільця R при n 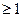, то, за означенням (3.1),отримаємо означення кільця R .

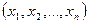Кожний елемент кільця R називають многочленом від n змінних над R і позначають f, g 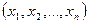і т.д.

Форма запису многочлена, яка не містить подібних членів, називають канонічною. Ця форма єдина з точністю до порядку членів.

Степенем члена многочлена називається сума . Число називається степенем даного члена відносно 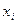. Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем називається старшим членом многочлена.

Якщо всі члени многочлена мають той самий степінь m, то многочлен називають однорідним многочленом степеня m (або формою степеня m).

Для многочленів від багатьох змінних поняття степеня члена вже недостатнє для встановлення єдиного порядку розміщення членів. Тому тут для зручного впорядкування членів користуються так званим лексикографічним принципом (за аналогією до впорядкування слів у словнику).

Розглянемо два довільні члени многочлена (1), (2). Якщо ці члени не подібні, то не всі відповідні степені та 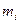рівні між собою, тобто існує хоча б одне таке натуральне число p, що 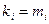при i =1,2,…, p -1, але 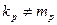. Якщо 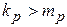, то член (1) називається вищим за член (2), якщо , то член (1) називається нижчим за член (2).

Розміщення членів многочлена, при якому вищі члени передують нижчим, називається лексикографічним. Перший за порядком член многочлена при лексикографічному розміщенні називають вищим членом многочлена.

Приклад.

Розмістити лексикографічно члени многочлена:

.

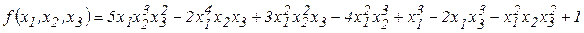Відповідь: .

б) Симетричні многочлени

Важливим класом многочленів від багатьох змінних є клас симетричних многочленів.

Многочлен називається симетричним відносно змінних 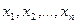, якщо внаслідок довільної перестановки змінних 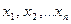утворюється многочлен, рівний даному.

Приклад.

.

Важливі приклади симетричних многочленів зустрічались в теоремі Вієта:

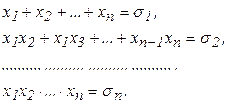
Ці симетричні многочлени називають елементарними симетричними многочленами.

Ясно, що якщо симетричний многочлен 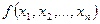містить деякий член 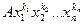, то він містить і член, утворений із даного довільною перестановкою показників.

Приклад.

В останньому прикладі та .

Очевидним є те, що якщо 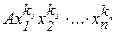є вищим членом симетричного многочлена, то .

Довільний симетричний многочлен від n змінних над полем Р можна однозначно подати у вигляді многочлена від елементарних симетричних многочленів з коефіцієнтами з поля Р.

Це твердження називають основною теоремою теорії симетричних многочленів.

Приклад.

f(x₁, x₂) = x₁²x₂ + x₁x₂² = (x₁ + x₂) x₁x₂ = σ₁σ₂.

Дата добавления: 2014-01-11