Дискретно - детерминированные модели

В тех случаях, когда предположение о конечномерности пространства состояний заменяется предположением о конечности числа его элементов, мы имеем дело с классом систем, анализ которых возможен с помощью чисто алгебраических методов. Этот класс систем носит название "класс конечных автоматов". Все последовательные вычислительные цифровые машины относятся к этому классу.

Конечный автомат A определяется как пятерка объектов

A = (X,Y.Q, D, L)

где Х - входной алфавит, т.е. совокупность возможных значений входа; У - выходной алфавит, Q - конечное множество внутренних состояний. Функции D и L определяют закон функционирования автомата: L

- определяет очередное внутреннее состояние в зависимости от предыдущего состояния и входа:

q(t+1) = D (x(t), q(t)), t=0,1,2.....

Функция λ определяет значение выхода

y(t) = L (x(t),q(t)).

Эти функции удобно задавать при помощи диаграммы переходов - ориентированного графа, вершина которого соответствует состояниям, а стрелки указывают в какое новое состояние переходит автомат под воздействием входного символа и каков будет выход (рис.3.1).

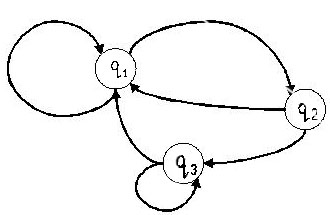
Рис. 3.1. Диаграмма переходов конечного автомата

Как отмечалось, ограничения вычислительного характера с неизбежностью вынуждаю нас явно или неявно сводить каждую системную задачу к конечномерному виду. Поэтому необходимы тщательное изучение и понимание алгебраической структуры подобных "конечных" описаний, которая основывается на теории конечных полугрупп.

Дата добавления: 2014-01-11