Дискретно - стохастические модели

Непрерывно - детерминированные модели

Со времен Ньютона динамические процессы описывали на языке дифференциальных уравнений, т.е. в терминах некоторых естественно выбранных переменных, таких как положение, температура, скорость и т.д. В общем виде такое описание может быть представлена как

dx/dt = f[x(t),u(t),t], x(0) = x 0, y(t) = h[x(t),u(t),t]

где х (t) - n-мерный вектор, компоненты которого описывают состояние системы в момент времени t, y(t)-p-мерный вектор наблюдаемых выходов системы, u(t)-m-мерный вектор входов системы, включая управляющие, и x (0) - начальное состояние системы.

Модели этого класса оказались достаточно обоснованными для анализа многих физических и технических задач. Однако возможность использования локального описания в случае менее изученных объектов в особенности систем социально-экономической природы, вовсе не очевидно.

Дискректно - стохастические модели классифицируются как вероятностные автоматы, которые отличаются от конечных автоматов тем, что функции D и L представляют собой распределение вероятностей, т.е. при данном состоянии q(t) и данном входе x(t) следующие состояния случайны. При этом известны вероятности попадания в каждое из состояний:

P{q(t+1)=qj, q(t)=qi, x(t)=xk} = pij

Сказанное относится и к выходу. Вероятность осуществления события q(t+1)=qj является условной и выполняется при условии, что имело место равенство q(t) =qi, x(t) = xk. Важным частным случаем является вероятностный автомат без входа и выхода. Такой автомат называется цепью Маркова. Цепь Маркова является частным случаем марковского случайного процесса с дискретным состоянием и дискретным временем. (Случайный процесс, протекающий в какой-либо физической системе, называется марковским или процессом без последствия, если он обладает следующим свойством: для любого момента времени to вероятность любого состояния системы в будущем (при t > to) зависит от ее состояния в настоящем (при t = to) и не зависит от того, когда и каким образом система пришла в это состояние).

Цепь Маркова задается множеством состояний q1, q2,..., qm и вероятностями перехода из состояния qi в qj:

pij = P{q(t+1)=qj | q(t)=qi}, t=0,1,2,3...

Их задают в виде матрицы

Если известно начальное состояние, то в последующие моменты времени цепь проходит через свои состояния случайным образом. Поэтому в каждый момент времени t=n можно говорить о вероятности pi (n) того, что цепь находится в состоянии i, i=1,2...m. Применение формулы полной вероятности дает соотношение

p_j (n+1) = 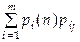, j=1,2,...m. (2.1)

По этой формуле можно найти распределение вероятностей состояния для любого момента времени.

Основным моментов теории марковских цепей является теорема Маркова о стационарном режиме. Оказывается, что при некоторых естественных предположениях цепь при больших n ведет себя так, что находится в каждом из своих состояний вполне определенную долю времени. Для формулировки теоремы обозначим через pij (n) - вероятность перехода цепи из состояния i в состояние j за n шагов.

Теорема Маркова. Если для любых двух состояний qi и qj выполняется pij >0, то существует такое распределение вероятностей {Pj}, j=1,2...m, что Pj(n)®Pj при n® 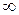. Это распределение единственно и не зависит от того, каким было начальное состояние цепи.

Распределение pj вычисляется с помощью соотношения (2.1). Переходя в нем к пределу, получим

(2.2)

Это система из m уравнений относительно m неизвестных Pj. Но на самом деле в ней только m-1 независимых уравнений. К ним надо добавить соотношение

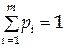
Дата добавления: 2014-01-11