Пример описания системы

Рассмотрим процесс производства подшипников роликового типа. Ставится задача определения оптимального промежутка времени между последовательными наладками оборудования.

Зависимость производственного процесса от этого фактора состоит в том, что для сокращения простоев, связанных с наладкой, и затрат на содержание бригад наладчиков, выгодно время между последовательными наладками оборудования увеличивать. Но если оборудование долго работает без наладки, растет доля бракованных подшипников. Увеличиваются потери рабочего времени и расход материалов.

Для надежных выводов требуется достаточно большое число экспериментов в цехе. Это нежелательно, так как отрицательно сказывается на производстве. В этих условиях естественно прибегнуть к имитационному моделированию.

Содержательное описание. Подшипник представляет собой устройство, содержащее наряду с другими деталями, ролики специального вида.

При сборке одного подшипника используется n роликов. Их число задано.

Основным фактором, определяющим качество подшипников, является однородность диаметров роликов. Из-за производственных погрешностей диаметры роликов имеют некоторый разброс. Подшипник считается годным, если разброс диаметров содержащихся в нем роликов не превосходит D (задано), в противном случае он считается бракованным.

В результате наблюдений установлено, что разброс диаметров увеличивается по мере увеличения продолжительности работы оборудования после очередной наладки. Для характеристики этой зависимости имеются статистические данные.

Интервал (0,Т) времени наблюдения был разбит на подинтервалы (0,t₁), (t₁,t₂)... (t_p-1,t_p). Ролики, изготовленные в течение каждого из них, разбивались на группы по диаметрам (d₁, d₂),(d₂, d₃).. (d_r1, d_r). Определялось количество попаданий в каждую группу h_ij. Полученные результаты представлены в таблице 4.1.

Таблица 4.1

Интервалы	Диаметры
d1-d2	d2 - d3		dr-1- dr
0 - t1	h11	h12	…	h1,r-1
t1- t2	h21	h22	…	h2,r-1
…			…
t1- t2	hp1	hp2	…	hp,r-1

Здесь hij - количество роликов, изготовленных в период (ti-1,ti), диаметры которых находятся в пределах (dj,dj+1).

Требуется дать математическую формулировку задачи о зависимости доли бракованных подшипников от длительности интервалов времени между последовательными наладками оборудования. Подготовить задачу для решения на компьютере, выполнить решение и дать интерпретацию полученных результатов.

Формализованная схема. Набор диаметров изготовленных роликов x1, x2... будем рассматривать как совокупность значений случайной величины X.

Для сборки очередного подшипника рассматривается случайная выборка (x1, x2,... xn) из n значений X. В этой выборке имеется наибольшее xmax = max(x1, x2,.., xn) и наименьшее значение xmin= min(x1, x2, xn).

Разность u = xmax - xmin назовем размахом выборки. Если u £D, то подшипник считается годным, а в противном случае бракованным.

Пусть за некоторое время изготовлено М подшипников, из которых m оказались годными, а (M -m) - бракованными. Тогда p = m / M – доля годных подшипников, q = (1 – m) / M - доля бракованных подшипников.

Теперь можно дать окончательное математическое описание случайной величины Х, задав закон ее распределения. Оказывается, что сведений, имеющихся в содержательном описании, недостаточно. Можно предполагать два варианта организации производственного процесса:

1. Изготовленные подшипники сразу идут на сборку. (Процессы обработки и сборки синхронизированы). В этом случае Х надо рассматривать как случайную величину, зависящую от времени. Минимальная информация для описания такой случайной функции - это среднее значение m(t)=M[X(t)] и корреляционная функция К(t1,t2)=M[X(t1) - m(t1)) (X(t2) - m(t2))]. Оценить K(t1,t2) по имеющейся таблице нельзя. Для ее вычисления нужно знать частоту совместного события

di £ X(ti) £ di+1; dj £ X(t2) £ dj+1

Таким образом, в этом случае необходимо дополнительное изучение процесса с целью получения этих данных.

2. Изготовленные орлики идут на склад. Для сборки берутся ролики со склада. В этом случае естественно считать, что при образовании случайной выборки в нее могут попасть ролики, изготовленные в любое время в пределах от 0 до Т (Т - интервал времени между наладками оборудования). Таким образом, в этом случае Х представляет собой обычную случайную величину, распределение которой зависит от периода Т.

Имеющихся в описании статистических данных достаточно для оценки этого закона распределения, но их необходимо переупорядочить. Нам нужно знать распределение диаметров для различных Т, т.е. для интервалов времени (0, t1), (0, t2)... (0, tp). Для каждого такого промежутка нужно оценить частоту Hij попадания диаметра в промежуток(dj-1, dj). Для их вычисления необходимо просуммировать числа в таблице 5.1. Переупорядоченная таблица принимает вид таблицы 4.2.

Таблица 4.2

Интервалы	Диаметры
d1-d2	d2 – d3		dr-1- dr
0 – t1	H11	H12	…	H1,r-1
0- t2	H21	H22	…	H2,r-1
…			…
0- tp	Hp1	Hp2	…	Hp,r-1

Предположим, что реальный процесс описывается второй схемой. Тогда по данным этой таблицы можно построить приближенное описание случайной величины Х - диаметр выбранного наудачу ролика, в предположении, что промежуток времени между наладками равен Т.

Для этого строится гистограмма Х: для каждого значения Т = ti определяется общее количество изготовленных роликов 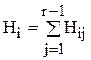Определяются частоты Hij /Hi и величины

,

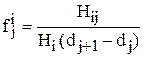используемые для построения гистограммы. Тогда в качестве плотности вероятности случайной величины Х можно приближенно выбрать эту гистограмму (рисунок 4.1)

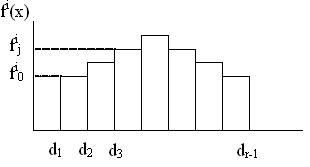
Рисунок 4.1 - Гистограмма случайной величины Х

Математическая модель. Хт - случайная величина, распределение которой зависит от параметра Т. Плотность вероятности Хт для Т = ti (i =1,2,...,r) задается величиной

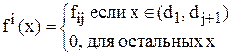; (x₁, x₂,..., x_n) - случайная выборка n значений Хт., xmax = max (x1, x2,..., xn), xmin = min (x1, x2,..., xn),

u = xmax - xmin

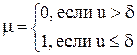
При данном Т рассматривается Мт - выборок и подсчитывается

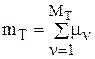; q(T) = 1 - m_т / M_т

Т - изменяется от 0 до Т с шагом .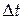

Алгоритм моделирования. Схема алгоритма моделирования, построенного в соответствии с математической моделью, имеет вид, показанный на рисунке 4.2.

┌───> 1. Tk=Tk-1+Dt

│ 2. если T<=Tk нет ---> Выдача результата ----> конец.

│ если да ----> fi (x)

│┌>┌> 3. проверка k < n, если нет ──────┐

││ │ если да ----> k=k+1 │

││ └─ 4. Формирование Xk │

││ 5. ny=ny+1 <─────────────────┘

││ 6. k=0

││ 7. Определение Xmax

││ 8. Определение Xmin

││ 9. U= Xmax - Xmin

││ 10. Проверка U £ D

││ если да ---> my =1

││ если нет --->my=0

││ 11. m Т + my

││ 12. Проверка ny < MТ

│└─────── если да

│ если нет

│ 13. q=1-(mТ/MТ) ────┐

└─────────────────┘

Рис. 4.2 - Схема алгоритма моделирования процесса производства

подшипников роликового типа

Дата добавления: 2014-01-11