Основные этапы построения имитационной модели

Автоматизированное конструирование моделей бизнес-процессов.

ПОСТРОЕНИЕ ИМИТАЦИОННОЙ МОДЕЛИ

Проверка адекватности модели и объекта

Проверка адекватности модели - этап очень важный, поскольку имитационные модели вызывают впечатление реальности и к ним проникаются доверием. Исходные предположения, на основе которых строится модель, часто бывают скрыты. Поэтому использование модели без проверки может привести в некоторых ответственных случаях к катастрофическим последствиям.

Для оценки адекватности модели могут быть использованы проверки трех видов.

При первой проверке убеждаются, что модель верна "в первом приближении". Убеждаются в том, что не будет ли модель давать абсурдные результаты, если ее параметры будут принимать предельные значения? При этом получаемые результаты должны иметь смысл.

Второй метод проверки адекватности состоит в проверке исходных предположений. Исходные предпосылки и положения не должны чрезмерно искажать и упрощать законы поведения объекта.

Третий вид проверок направлен на выявление ошибок в преобразованиях информации в модели от входа к выходу.

Последние два вида проверок могут потребовать привлечения статистических методов проверок различных гипотез.

В другом подходе способов оценки имитационной модели различают три категории:

1) верификацию, используя которую экспериментатор хочет убедиться, что модель ведет себя так, как было задумано;

2) оценку адекватности - проверку соответствия между поведением реальной системы и поведением модели;

3) проблемный анализ - формулирование статистически значимых выводов на основе данных, полученных путем машинного моделирования.

Таким образом, вопрос оценки адекватности модели имеет две стороны:

- приобретение уверенности в том, модель ведет себя таким же образом, как и реальная система;

- установление факта, что выводы, полученные из экспериментов с моделью, справедливы и корректны.

План лекции

1. Основные этапы построения имитационной модели

2. Структурный анализ процессов на объекте экономики.

3. Функциональная модель и ее диаграммы. Типы связей между функциями.

4. Уровни детализации функциональной модели фирмы.

5. Процесс создания двух взаимосвязанных моделей: функциональной структурной и динамической имитационной.

Как уже отмечалось, в отличие от других видов и способов математического моделирования с применением ЭВМ имитационное моделирование имеет свою специфику: запуск в компьютере взаимодействующих вычислительных процессов, которые являются по своим временным параметрам - с точностью до масштабов времени и пространства – аналогами исследуемых процессов.

Имитационное моделирование как особая информационная технология

состоит из следующих основных этапов.

1. Структурный анализ процессов. Проводится формализация структуры сложного реального процесса путем разложения его на подпроцессы, выполняющие определенные функции и имеющие взаимные функциональные связи согласно легенде, разработанной рабочей экспертной группой. Выявленные подпроцессы, в свою очередь, могут разделяться на другие функциональные подпроцессы. Структура общего моделируемого процесса может бьггь представлена в виде графа, имеющего иерархическую многослойную структуру, в результате появляется формализованное изображение имитационной модели в графическом виде.

Структурный анализ особенно эффективен при моделировании экономических процессов, где (в отличие от технических) многие составляющие подпроцессы не имеют физической основы и протекают виртуально, поскольку оперируют с информацией, деньгами и логикой (законами) их обработки.

2. Формализованное описание модели. Графическое изображение имитационной модели, функции, выполняемые каждым подпроцессом, условия взаимодействия всех подпроцессов и особенности поведения моделируемого процесса (временная, пространственная и финансовая динамика) должны быть описаны на специальном языке для последующей трансляций. Для этого существуют различные способы:

• описание вручную на языке типа GPSS, Pilgrim или любом универсальном языке программирования, например, на Visual Basic. Последний очень прост, на нем можно запрограммировать элементарные модели, но он не подходит для разработки реальных моделей сложных экономических процессов, так как описание модели средствами специализированных имитационных систем компактнее аналогичной алгоритмической модели на Visual Basic в десятки-сотни раз;

• автоматизированное описание с помощью компьютерного графического

конструктора во время проведения структурного анализа, т.е. с очень незначительными затратами на программирование. Такой конструктор, создающий описание модели, имеется в составе специализированных систем моделирования.

3. Построение модели (build). Обычно это трансляция и редактирование связей (сборка модели), верификация (калибровка) параметров. Трансляция осуществляется в различных режимах:

• в режиме интерпретации, характерном для систем типа GPSS, SLAM-II, ReThink;

• в режиме компиляции (характерен для системы Pilgrim).

Каждый режим имеет свои особенности.

Режим интерпретации проще в реализации. Специальная универсальная

программа-интерпретатор на основании формализованного описания модели запускает все имитирующие подпрограммы. Данный режим не приводит к получению отдельной моделирующей программы, которую можно было бы передать или продать заказчику (продавать пришлось бы и модель, и систему моделирования, что не всегда возможно).

Режим компиляции сложнее реализуется при создании моделирующей системы. Однако это не усложняет процесс разработки модели. В результате можно получить отдельную моделирующую программу, которая работает независимо от системы моделирования в виде отдельного программного продукта.

Верификация (калибровка) параметров модели выполняется в соответствии с легендой, на основании которой построена модель, с помощью специально выбранных тестовых примеров.

4. Проведение экстремального эксперимента для оптимизации определенных параметров реального процесса.

2. Структурный анализ процессов в объектах экономики. Функциональная модель и ее диаграммы. Типы связей между функциями.

Основа концепции имитационного инструментария, с помощью которого можно проводить структурный анализ и имитационное моделирование, заключается в механизмах, позволяющих агрегировать элементарные процессы и устанавливать между ними функциональные связи (причинно-следственные, информационные, финансовые и иные). Ниже предлагается сетевая концепция, существенно отличающаяся от аналитического аппарата, рассмотренного в литературе по теории массового обслуживания, использующая удачные результаты теории стохастических сетей и численные методы, основанные на диффузной аппроксимации процессов массового обслуживания.

Эта концепция разработана, в первую очередь, для последующей реализации имитационных механизмов в рамках специального пакета имитационного моделирования. Она предназначена для верификации работоспособности пакета, для оценочных расчетов при отладке имитационных моделей, но не предназначена для практических расчетов показателей риска по аналитическим формулам.

Идею предлагаемой концепции рассмотрим на примере из конкретного проекта «Открытое образование» («е-образование»), реализуемого под патронажем Международной академии открытого образования (МАОО).

Пример: учебные процессы в открытом образовании. Учебный процесс - это понятие, охватывающее всю учебную деятельность классического университета. Учебный процесс состоит из многих компонентов: процесса обучения студента по конкретной специальности в течение пяти лет, семестрового учебного процесса на потоке, процесса изучения дисциплины. Классический университет имеет жесткий избыточный набор ресурсов, который позволяет реализовать учебный процесс в любой его интерпретации. Однако такой фиксированный набор приводит к издержкам планирования, к удорожанию обучения студента без гарантий высокого качества.

В открытом образовании работают специалисты, имеющие квалификацию не ниже, чем в классическом университете. Единственное, что их отличает, - это различные образовательные технологии (классическая и комплексная). Процессом изучения дисциплины (далее - процессом) в распределенном институте назовем неделимую функцию освоения дисциплины студентом по утвержденной программе. Для реализации процесса необходимы различные ресурсы.

В системе открытого образования ресурсы используются в распределенном режиме. Ресурсы распределенного института можно поделить на два типа: интеллектуальный ресурс (учитель) и учебный ресурс (далее - просто ресурс).

Учителя - это преподаватели кафедр, тренеры учебно-тренировочных фирм, тьюторы-консультанты. Учителя предметно относятся к разным распределенным кафедрам через механизм «аттестации».

Ресурсы - это комплекты учебно-практических пособий, студии (если есть дистанционная фаза типа телеконференции), режимы Интернет-доступа, аудитории (если есть очная фаза) и другие, без которых обучение студента может не состояться.

Процесс запущен, если возникла необходимость изучения дисциплины и распределенный институт имеет для этого ресурсы. Запуск процесса не означает, что в любой момент времени будет хотя бы один студент, изучающий эту дисциплину. Соответственно процесс может быть снят (или отменен).

Далее будем полагать, что распределенный институт ориентирован прежде всего на индивидуализацию обучения студента. Поэтому с учетом случайных явлений, не зависящих от распределенного института, при массовом обслуживании студентов возможны технологические задержки: очереди к учителям и задержки из-за временной нехватки ресурсов. Возникает задача определения такого числа ресурсов, при котором процесс обучения по конкретйой специальности имел бы продолжительность не хуже заданной с учетом технологических задержек.

При реализации обучения по специальности процессы могут иметь причинно-следственные связи. Поэтому можно говорить о том, что они образуют направленный граф (рис. 5.1).

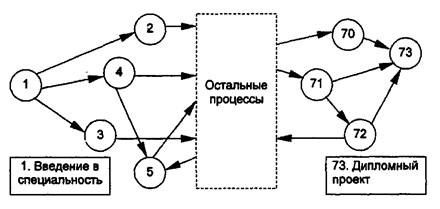
Рис.5.1. Сеть процессов при обучении по специальности

Применение методов сетевого планирования и управления невозможно; основная трудность - это циклы. Циклы возникают по двум причинам: студенты обучаются не по жесткому учебному плану (возможны различные индивидуальные планы), для отстающих студентов организуется повторное обучение (возврат к пройденной ранее, но не защищенной дисциплине для ее более глубокого изучения). Относительно пути студента по графу в каждый момент времени он находится в определенном текущем процессе - в узле графа. Процесс, который передал студента в текущий процесс, назовем производителем, а процесс, который примет студента после завершения текущего, назовем потребителем.

Рассмотрим возможные диаграммы состояний процесса (рис. 5.2). Если мощности ресурсов бесконечны либо каждый процесс используется вместе с постоянно закрепленными за ним ресурсами, то возможны два состояния (рис.5.2,а): ожидание студентов (ЖС) и вьшолнение процесса изучения дисциплины (ПУ). В таких ситуациях не возникает необходимости в незапланированных ресурсах: у студента есть учебный план. В состояние ПУ процесс попадает, получив студента от процесса-производителя. После изучения дисциплины студент переходит к процессу-потребителю и попадает в состояние ЖС, если какой-либо производитель не подготовил следующего студента.

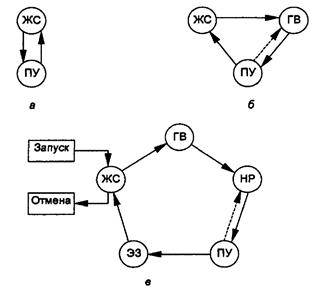
Рис. 5.2. Диаграммы состояний процессов (курсов):

а - мощности ресурсов бесконечны; б - мощности ресурсов конечны;

в - мощности ресурсов конечны, есть накладные расходы времени;

ЖС - ждет студентов; ГВ - готовится к выполнению; НР - нужны ресурсы;

ПУ - учеба по дисциплине; ЭЗ - экзамен, зачет

В более peaльном случае (рис. 5.2,б) при конечных мощностях глобальных ресурсов появляется состояние ожидания ресурса, когда процессу (точнее, студенту в процессе изучения дисциплины) нужны ресурсы (HP). В условиях реального университета, когда обучение контролируется, а выделение ресурсов и их возвращение осуществляется с помощью процессов планирования и распределения ресурсов, вводятся еще два состояния (рис.5.2,в): подготовка к выполнению (ТВ) и завершение выполнения - контрольные мероприятия, экзамены, зачеты (ЭЗ).

Когда возникает потребность в незапланированных ресурсах, то возможны обратные переходы типа ПУ-НР (рис. 5.2,б, 5.2,в). Такие переходы могут привести к блокировкам, которые можно разрешить с помощью известных решений задачи взаимного исключения.

3. Функциональная модель и ее диаграммы. Типы связей между функциями.

Во время подготовки к выполнению (ГВ) осуществляется планирование ресурсов, а после завершения (ЭЗ) - возврат ресурсов в распоряжение планирующих и распределяющих процессов. Организация и взаимосвязь различных компонентов системы открытого образования может быть рассмотрена относительно управления процессами в следующих подразделениях университета (рис. 5.3):

• управления учебной и учебно-методической работой (УУМР), которое ведает всеми ресурсами, относящимися к учебному процессу;

• дирекции распределенного университета, которая совместно с территориально-распределенными филиалами университета (партнерами) отвечает за реализацию учебного плана;

• учебно-методологического совета (УМС), который работает при дирекции в качестве коллегиального совещательного органа для постоянного соверщенствования государственных образовательных стандартов (ГОС), изменяющихся примерно раз в пять лет, и учебного плана, который корректируется ежегодно (в рамках действующего ГОС);

• кафедр (распределенных кафедр открытого образования). Кафедры - это обладатели интеллектуального ресурса (профессорско- преподавательского состава, тренеров (тьюторов-консультантов), аспирантов, докторантов и других преподавателей).

Рис. 5.3. Функциональные взаимосвязи организующих объектов

в учебном процессе распределенного института

Далее перейдем к оценке времени изучения студентами дисциплин учебного плана. Время прохождения всех дисциплин учебного плана студентом - это время пребывания заявки в стохастической сети (см. рис. 5.1). Заявки в такой сети будем насыщать «транзактами», чтобы отличать от других элементарных заявок.

Транзакт, попадая из одного узла сети (процесс-производитель) в другой узел (процесс-потребитель), свидетельствует о необходимости изучения студентом следующей дисциплины учебного плана. После этого процесс-потребитель выводится из состояния ЖС и попадает в состояние ГВ. После вьщеления ресурсов (HP), выполнения функции (ПУ) и завершения выполнения контрольных мероприятий (ЭЗ) транзакт появляется на выходе узла-производителя, а процесс возвращается в состояние ЖС. Случайный интервал времени, ограниченный моментом выхода процесса из состояния ЖС в начале изучения дисциплины и ближайшим моментом попадания в это состояние, назовем интервалом активности процесса. Длительность пребывания транзакта в соответствующем узле - это интервал активности. Для оценки времени реакции системы открытого образования, реализуемой в рамках распределенного института по учебному плану, необходимо уметь рассчитывать значения интервалов активности всех процессов, входящих в состав сети.

4.Уровни детализации функциональной модели фирмы.

Оценка интервала активности процесса. Далее построим итерационную процедуру, позволяющую провести соответствующие оценки. Обозначим А - начало очередной итерации; Б - конец очередной итерации.

А. Начало итерации. Пронумеруем N узлов стохастической сети, характеризующих конкретный план, индексами j и предположим справедливость допущений:

1) известны средние значения всех интервалов активности t_нj. j=1,2,..., N (только в каком-то приближении, так как их необходимо рассчитать);

2) известны вероятности поступления транзакта из каждого процесса-производителя в любой процесс-потребитель 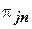, j,n=1,2… N; эти вероятности определяются исходя из параметров набора учебных планов, индивидуальных схем обучения и числа студентов, проходящих через систему открытого образования;

3) сеть, отображающая конкретный учебный план, является полнодоступной с матрицей передач П=[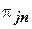], причем вероятность поступления транзакта в процесс-потребитель п в течение интервала времени (t, t+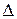_t,) является линейной комбинацией с постоянными коэффициентами 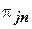вероятностей появления заявок на выходах вершин-производителей с номерами j.

Такие допущения могут быть в какой-то степени справедливы, если учебный процесс находится в стационарном режиме (если переходные процессы и были, то они завершились). Поэтому при их выполнении можно получить среднее время изучения всех дисциплин учебного плана по формуле для замкнутых сетей:

где t_иj - средняя длительность интервала активности; 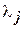- интенсивность запросов на курс с номером j; - интенсивность поступления потока студентов, желающих обучаться по данному учебному плану.

Поэтому для оценки времени выполнения учебного плана необходимо знать средние значения интервалов активности всех процессов.

Для анализа интервала активности необходимо рассмотреть «нетрадиционную модель» массового обслуживания. Введем условные обозначения параметров временных интервалов:

t_ж - процесс ждет студентов (состояние ЖС);

t_Г - готовится к выполнению (состояние ГВ);

tн - процессу нужны ресурсы (состояние HP);

t_П - процесс учебы (состояние ПУ);

d_П - дисперсия процесса учебы;

tэ, - экзамен, зачет, контрольное мероприятие (состояние ЭЗ);

t_р - длительность ожидания запроса в очереди к ресурсу;

t_и - длительность интервала активности процесса;

tс - основная составляющая интервала активности tc = t „ - t r;

to - длительность ожидания первого элемента ресурса;

tr, - длительность ожидания какого-либо ресурса;

tq - длительность ожидания обслуживания в очереди к ресурсу;

t_s, - длительность обслуживания в очереди к ресурсу;

t_v - время ожидания из-за нехватки элементов ресурса;

t_w - время ожидания запрошенного элемента ресурса;

Сr - коэффициент вариации времени ожидания ресурса;

Cs -коэффициент вариаций времени обслуживания в очереди к ресурсу;

Са - коэффициент вариации интервала запросов к ресурсу.

На интервале активности процесс может находиться в состояниях ГВ, HP, ПУ и ЭЗ. Будем считать, что ресурсы выделяются во время пребывания в состоянии HP (интервал tнj,), а освобождаются все сразу - в конце интервала пребывания в состоянии ЭЗ (по истечении tэj), оба эти интервала - детерминированные величины. Интервал активности равен:

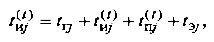
где 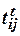- длительность пребывания в состоянии HP; 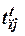-длительность пребывания в состоянии ПУ; j - номер процесса, j=1,2,....,N, (t) - индекс, показывающий случайный характер индексируемой величины.

Будем считать, что величины tгj и tэj известны, а интервал /^^ задан с помощью математического ожидания Гп и дисперсии da. Интервал 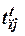можно определять с помощью одного из трех возможных способов:

1) исходя из характеристик распределенного института (головного университета, осуществляющего открытое образование);

2) с помощью хронометрирования;

3) если институт осуществляет приоритетное обслуживание для некоторых категорий учащихся, то 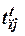- это цикл обслуживания; методика определения цикла обслуживания для потоков типа пуассоновского или группового.

Предположим, что в распоряжении института имеется М глобальных ресурсов, используемых при обучении. Мощность каждого ресурса - Si элементов, а для выполнения процесса (изучения курса) у предварительно необходимо выделить Rij элементов каждого ресурса. Причем 0 < R_ij < Si, i =1,2.. M,j=1,2.. N.

Поставим в соответствие началу интервала активности момент появления транзакта на входе модельной системы, изображенной на рис. 1.10,а. Этот транзакт попадает на вход генератора, на каждом i-м выходе которого через время t г j появятся порции Rij заявок, которые распределяются по Si, очередям. Длительность обслуживания в каждой очереди - это интервал времени, начинающийся в момент вьщеления процессу первого элемента ресурса i из набора свободных ресурсов и заканчивающийся моментом возвращения всех Rij элементов в этот набор (каждому ресурсу соответствует свой менеджер обслуживания, контролирующий очередь).

Через какой-то интервал времени

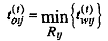
на входе счетчика появится первая удовлетворенная заявка очереди i-го ресурса. После этого проходит еще Rij -1 случайных интервалов, пока не появятся остальные заявки (каждая соответствует одному выделенному элементу). Если считать, что интенсивность освобождения процессами элементов стационарна, то каждый из Rij -1 интервалов в среднем равен tri/ Si, где t_ri = М [t_ri^(t)].

Через время

появится последняя заявка, соответствующая выделению последнего из запрошенных r_ij элементов i-ro ресурса. После чего учебный процесс выполняется (за время 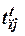) и завершается контрольными мероприятиями (за время tэj). Поток заявок, поступающий на вход рассматриваемой модели, - неординарный с интенсивностью 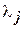. Мы не рассматриваем классический учебный процесс классического университета, строящийся по принципу объединения: специальность<->учебный план <->учебное расписание контингент (группы студентов).

Рис. 5.4. Модель анализа интервала активности процесса:

а - схема массового обслуживания в пределах интервала активности;

б- временные диаграммы элементарных процессов

Однако есть две причины, позволяющие предположить возникновение в модели режима открытого образования случайных групп в потоках траизактов:

• один студент может привести несколько студентов (а в модели один транзакт может породить группу других транзактов);

• в учебном плане могут быть циклы.

Сеть процессов, образующих учебный план, - довольно сложная, полнодоступная. Поэтому в практических расчетах будем считать, что поток групп - пуассоновский, а размер группы распределен по закону обобщенного распределения фланга.

Одно из свойств групповых потоков заключается в том, что превосходит математическое ожидание интервала между заявками, поэтому коэффициент вариации с > 1. Формула для оценки среднего размера группы заявок при обобщенном распределении Эрланга имеет вид

Это соотношение позволяет отслеживать появление групповых потоков в реальных системах или в их имитационных моделях. Особенность обобщенного распределения Эрланга заключается в том, что его применение позволяет выполнить расчет на худший случай (при перегрузках).

Далее воспользуемся свойствами полученного распределения. Поэтому применим гипотезу Л. Клейнрока о независимости не к потокам заявок, а к потокам групп заявок. Коэффициент вариации интервала поступления с_j в групповом потоке такого типа не меньше единицы. Исходя из свойств рассмотренного распределения, средний размер случайной группы ^ связан с коэффициентом вариации соотношениями:

Средний размер группы, поступающей в одну очередь, равен:

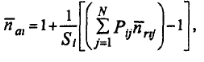
Где вероятность того, что запрос на выделение элемента i-го ресурса поступил от j-го процесса:

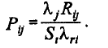
Предположим, что известна вероятность ненулевой задержки в очереди (в режиме перегрузок) и среднее значение tcj = t_иj+t_rj.. По правилу расчетов для объединения процессов с учетом формул диффузной аппроксимации получим среднее время обслуживания очереди:

Б. Конец итерации. Из временной диаграммы на рис. 5.4,б следует:

Уточнив значения, известные в начале итерации с какой-то погрешностью, итерацию можно повторить, пока процесс не сойдется к результатам с приемлемой точностью. Таким образом, методом последовательных приближений можно получить интересующие нас параметры интервала активности. Расчеты выполняются метод(последовательных приближений с использованием рекурсивной функции, написанной на языке C++.

Предлагаемый аппарат описания процессов в узлах стохастической сети распространяется на другую предметную область, более широкую по сравнению с классическими моделями. Предложенные выше формулы предназначены только для предварительных оценок средних величин в установившемся режиме. Они не пригодны для расчетов в режиме переходного процесса: сложный переходный процесс обычно изучается с помощью имитационной модели. Однако рассмотренные выше временные диаграммы обладают высокой универсальностью.

Все процессы, независимо от количества уровней структурного анализа, объединяются в виде направленного графа. Пример изображения модели в виде многослойного иерархического графа, полученного при структурном анализе процесса, показан на рис. 5.5.

Рис. 5.5. Многослойный граф модели

Процесс построения графа имитационной модели сопровождается структурным анализом исследуемого процесса. При структурном анализе возникает задача перехода между слоями: нижние слои модели содержат декомпозицию узлов, расположенных выше. Декомпозиция - это детализация одного узла с помощью совокупности других узлов.

Существуют четыре разновидности декомпозиции процессов:

1) общий случай декомпозиции сложного процесса с помощью узлов типа down;

2) декомпозиция процессов перечисления денег (платежей, бухгалтерских проводок и др.) с помощью узлов типа pay;

3) декомпозиция процессов выделения ресурсов с помощью узлов типа rent;

4) абстрактное объединение группы процессов в один псевдопроцесс с помощью виртуального (мнимого, не существующего в реальности) узла parent без образования нового узла.

Общая схема взаимодействия между слоями модели показана на рис. 5.5. Здесь рассматривается декомпозиция реальных узлов pay, rent и down. Управление переходами между слоями модели при многоуровневой декомпозиции основано на применении виртуального узла parent,

6. Автоматизированное конструирование моделей бизнес-процессов.

В последние годы все большее распространение получают CASE-средства, позволяющие автоматизировать процессы проектирования, разработки и поддержки программных приложений:

• компьютерных экономико-математических моделей;

• экономических информационных систем;

• вычислительных программ прикладной математики экономического назначения.

САSЕ-средства активно используют методологию структурного анализа, предусматривающую наглядное и эффективное проектирование системы путем вьщеления ее составляющих и их последовательного рассмотрения. Описание системы начинается с общего обзора и выделения основных ее компонентов или процессов. Для визуального представления создается первый уровень или слой, на котором отображаются выделенные процессы и их взаимосвязи. Далее для ряда процессов может быть проведена детализация, в свою очередь выделяющая новые процессы в их структуре. Так, последовательным усложнением описания объекта и его процессов разработчик достигает необходимой детализации. Глубина детализации определяется как необходимой точностью, так и набором исходных данных. В процессе структурного анализа выявляется иерархическая структура модели.

Рассмотренный ниже декомпозиционный подход реализуется в программных CASE-пакетах в различных вариациях, поскольку существует достаточно широкий круг задач, для которых схожие методы могут быть применены. Однако все CASE-пакеты предоставляют пользователю инструментарий работы с проектом, опирающийся на мощные современные графические средства отображения информации в виде графов, диаграмм, схем и таблиц.

Одним из достаточно интересных и полезных применений CASE-средств является не только их интеграция в процессы проектирования, разработки и поддержки структуры программного проекта, но и автоматизация процесса создания или генерации программного кода. Использование CASE-средств, дополненных такой возможностью, имеет ряд несомненных преимуществ перед простым кодированием, поскольку позволяет:

• отвлечься от кодирования данных и обратить большее внимание на структуру разрабатываемой системы;

• избежать некоторых ошибок за счет автоматического контроля;

• ускорить процесс проектирования и разработки проекта.

Теперь рассмотрим CASE-технологии применительно к системе имитационного моделирования. Для создания имитационной модели в отсутствие CASE-средств разработчику приходится писать программный код, использующий языковые средства системы моделирования Pilgrim. Модель имеет стандартную структуру. Внутри текста модели содержатся обращения к функциям Pilgrim, но может быть и произвольный C++ код.

Учитывая, что текст модели обрабатывается препроцессором и стандартным компилятором C++ (Microsoft, Borland и др.), можно выделить ряд проблем, возникающих перед пользователем при описании модели в операторах Pilgrim, а именно:

• необходимо знать элементы языка C++;

• нужно иметь отчетливое представление о структуре программы,

опирающейся на библиотеку Pilgrim;

• требуется знать функции описания узлов и их параметров;

• имеется вероятность появления ошибки в порядке перечисления позиционных параметров, причем ошибка может бьггь не замечена компилятором C++, в результате чего модель будет выполняться, но иметь на выходе неправильные результаты. Обнаружение такой ошибки тем сложнее, чем большее количество узлов имеет модель;

• сложность описания больших моделей. Поскольку модель любого размера выглядит как простое линейное перечисление узлов и условий переходов между ними, то, чем больше текст модели, тем он сложнее воспринимается пользователем.

Конструктор моделей Pilgrim (далее - конструктор) позволяет автоматизировать процесс создания графа модели и автоматически генерировать код Pilgrim-программы. Тем самым снимаются отмеченные выше проблемы, возникающие при ручном кодировании модели в виде Pilgrim-файла:

• автоматическая генерация программного кода позволяет пользователю не задумьшаться о структуре и синтаксисе программы, уделяя все внимание структуре и параметрам самой модели и ее узлов;

• генерация функций описания узлов конструктором исключает ошибки, связанные с неправильной последовательностью указания позиционных параметров или пропуском некоторых из них;

• анализируя модель, конструктор не позволяет пользователю выполнять заведомо неверные действия, а также предупреждает о возможных ошибках;

• поддержка конструктором множества плоскостей обеспечивает создание иерархических моделей, что может быть очень удобно при выполнении моделей с большим количеством узлов. Действительно, не только восприятие, но и отображение больших моделей в виде плоского одноуровневого графа на бумаге или экране монитора достаточно затруднено.

Дата добавления: 2014-01-11