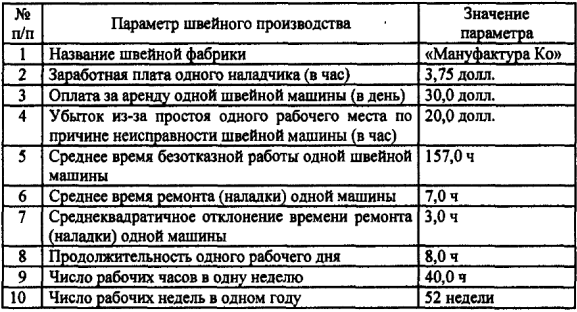
Параметры швейной фабрики

ИМИТАЦИОННЫЕ РЕШЕНИЯ ЗАДАЧ МИНИМИЗАЦИИ ЗАТРАТ

Рассмотрим модель, которая относится к замкнутым имитационным моделям. Предположим, что мы открыли собственную швейную фабрику «Мануфактура Ко». На этой фабрике есть швейный цех, где имеются 50 рабочих мест со швейными машинами. Машины выходят из строя и требуют ремонта. Поэтому на фабрике есть ремонтный цех, в котором работают специалисты - наладчики машин.

Среднее время безотказной работы одной машины 157,0 ч. Естественно допустить, что это время - случайная величина, распределенная по экспоненциальному закону в соответствии с предельной теоремой о суперпозиции потоков. Допущение основано на том, что машина - сложное устройство, состоящее из сотен деталей и узлов, которые могут выйти из строя.

Среднее время ремонта машины равно 7,0 ч; среднеквадратичное отклонение времени ремонта - 3,0 ч. В соответствии с центральной предельной теоремой считаем, что время ремонта, состоящего из многих последовательных элементарных операций, распределено по нормальному закону.

Сформулируем следующую задачу: сколько нужно арендовать резервных машин j (дополнительно к 50 собственным) и сколько необходимо нанять наладчиков i, чтобы сделать минимальными затраты на производство, связанные с ремонтом и наладкой машин?

Все исходные данные для решения поставленной задачи сведены в табл. 8.3. В качестве денежной единицы выберем американский доллар (только для определенности).

Таблица 8.3

Сначала попытаемся решить эту задачу без применения имитационной модели. Допустим, что необходимо j дополнительных машин, которые будем арендовать на каком-либо складе.

Нетрудно представить, что каждая машина находится в двух состояниях:

1) находится в швейном цехе и работает;

2) находится в ремонтном цехе, неисправна и ремонтируется наладчиками.

Средняя длительность такого цикла равна 157 + 7 = 164. Поэтому введем в рассмотрение полезную загрузку одной машины р= 157/164 = 0,957.

Составим простое уравнение, показывающее, сколько нужно иметь дополнительных машин, чтобы все 50 мест не простаивали: 50 = р(50+у).

Решение этого уравнения элементарно: у = 50(1-р) = 2,15 машин. Однако решение должно быть целочисленным. Поэтому округляем в большую сторону и получаем целое числом' = 3. Время ремонта составляет 7 ч, Учитывая, что постоянно будут неисправны 3 машины, а рабочий день составляет 8 ч, наймем трех наладчиков, которые будут хорошо загружены в течение дня (два наладчика могут не справиться с потоком машин, поступающих в ремонт). Получили искомую величину: / = 3.

Если поступим в соответствии с полученным решением и будем проводить натурное моделирование, собирая в течение длительного периода времени (не менее года) хронометрическую и финансовую информацию, то увидим, что решение, полученное выше, неверное.

Основная ошибка заключалась в гипотезе о том, что машины находятся в двух состояниях. На самом деле таких состояний четыре (рис. 8.7). Выбранные выше состояния (исправная работа и ремонт) осуществляются в двух цехах: швейном и ремонтном. В начальный момент, при организации производства, все машины были исправны.

Введем в рассмотрение следующие переменные, которые далее будут использоваться в модели:

• Nowon - количество рабочих мест в швейном цехе и соответственно

количество собственных швейных машин;

• Arend - число арендуемых дополнительных машин для замены

вьппедших из строя;

• Men - количество наладчиков, производящих ремонт (наладку)

швейных машин.

Отметим все значимые для задержек состояния в табл. 8.4.

Таблица 8.4

Дата добавления: 2014-01-11