Модель производственной фирмы

Результаты моделирования

2.1. Предварительный план проекта производственной фирмы

Обсуждается проект создания производственной фирмы, которая будет производить изделия по заказам потребителей. Количество заказов заранее неизвестно. Можно только предположительно указать среднее число заказов в единицу времени (например, в день).

В таком случае следует принять допущение о том, что поток заказов является простейшим, а это означает, что время между соседними заказами представляет собой случайную величину с показательным распределением.

Предполагается, что в технологическом процессе производства будет участвовать несколько цехов. Каждый из них будет выполнять определенную часть операций по изготовлению изделия, а из последнего цеха будет выпускаться готовое изделие. Сколько будет цехов и какую часть времени изделие будут находиться в каждом из них, пока неизвестно. Желательно, чтобы структура предприятия была оптимальной в смысле обеспечения наибольшей прибыли. Пока можно лишь указать среднее время на изготовление одного изделия. Оно складывается из среднего времени работы с изделием в различных цехах. Можно также ориентировочно указать величину максимального разброса времени изготовления изделия в процентах от его среднего значения.

В этих условиях целесообразно принять допущение о том, что время изготовления изделия в каждом цехе является случайной величиной с нормальным распределением. Среднее время работы с изделием для каждого цеха должно быть задано. Разброс времени изготовления изделий можно характеризовать относительным значением среднего квадратического отклонения времени работы с изделием, постоянным для всех цехов.

В качестве показателя эффективности предполагается использовать величину средней прибыли. Ее можно определить как произведение среднего числа изготовленных изделий на цену одного изделия за вычетом общих затрат на организацию производства.

Можно ориентироваться на среднюю прибыль, но предпочтительнее выбрать минимальную гарантированную прибыль с заданным уровнем гарантии, которая учитывает разброс возможных величин прибыли относительно ее среднего значения.

Наиболее неопределенной представляется структура будущего предприятия. Существует множество вариантов распределения ресурсов по цехам. Однако, можно сформировать такой числовой параметр, который отражал бы изменения в структуре предприятия. Для этого нужно выбрать такую переменную, которая была бы чувствительна к изменению структуры производства и представляла бы собой непрерывную величину, меняющуюся в некотором диапазоне (например, в интервале (0,1)). Для этого придется сделать дополнительные допущения.

Прежде всего будем считать суммарное среднее время работы всех цехов по изготовлению одного изделия величиной постоянной и заданной. Для каждого варианта структуры предприятия будем считать, что средние времена работы в цехах образуют убывающий ряд чисел. Тогда среднее время работы в первом цехе будет максимальным, а в последнем цехе - минимальным. Если разделить разность между максимальным и минимальным временем на общее среднее время работы с изделием, то получим безразмерный параметр, принимающий значения в интервале (0,1). Этот параметр можно назвать числовым фактором.

Равенство числового фактора нулю означает, что время работы с изделием во всех цехах одинаково. Это реализация конвейерного способа производства.

Равенство числового фактора единице означает, что среднее время работы в первом цехе (максимальное среднее время работы) численно равно общему среднему времени работы предприятия по изготовлению одного изделия. Это случай, когда весь производственный процесс сосредоточен в одном цехе.

Все остальные возможные варианты являются промежуточными, им соответствуют значения числового фактора Fact удовлетворяющие неравенству: 0 < Fact < 1.

Подсчитаем теперь число входных переменных, которые будет иметь модель производственной фирмы. Это будет зависеть от числа цехов. Если ограничить число цехов четырьмя, то можно насчитать 7 входных переменных:

• интенсивность потока заказов;

• среднее время работы с изделием в каждом цехе (для четырех цехов);

• относительная величина среднего квадратического отклонения времени работы с изделием в любом цехе;

• цена одного изделия;

• общая стоимость затрат на организацию производства;

• продолжительность периода функционирования производственной фирмы;

• число случайных реализаций моделируемого процесса.

Числовой фактор не является независимой входной переменной. Числовой фактор определяется после выбора значений среднего времени работы с изделием в каждом цехе. Он является в модели выходной переменной наряду со средним числом изготовленных изделий, средней прибылью и средним квадратическим отклонением прибыли.

Определим теперь класс моделей к которому можно отнести создаваемую модель. Очевидно, что это алгоритмическая модель одноканальной, многофазной системы массового обслуживания с однородными заявками и неограниченным ожиданием.

2.2. Концептуальная модель

Имеется производственная фирма, которая осуществляет выпуск сложных изделий по заказам потребителей. Технологический процесс предусматривает изготовление отдельных узлов и агрегатов с помощью различного оборудования, которое может размещаться в нескольких цехах. Количество цехов Nц- величина переменная, изменяющаяся от 1 до 4.

Поток заказов - простейший (пуассоновский) с известным средним числом заказов в день - L_z

Случайная величина времени изготовления одного изделия складывается из случайных величин времени изготовления агрегатов в каждом цехе, имеющих нормальное распределение. Среднее значение времени работы (времени «обслуживания» изделия) в j-м цехе T_обj для каждого варианта структуры предприятия cчитается заданным. Суммарное среднее время изготовления изделия T_s является постоянным. Разброс времени работы в каждом цехе характеризуется относительным средним квадратическим отклонением 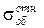, постоянным для всех цехов. На выпуск продукции оказывает влияние структура предприятия, т. е. количество цехов и распределение ресурсов по цехам. Число возможных вариантов структуры бесконечно. Поэтому для исследования влияния структуры фирмы на эффективность производственного процесса необходимо выбрать параметр или числовой фактор, который свел бы количество расчетных вариантов к обозримому числу.

В качестве такого числового фактора предлагается ввести следующее выражение:

Fact = {MAX(Т_обj) - MIN(T_обj)} / Т_s (j=1, 2, 3,4),

где MAXt(T_обj)) - максимальное среднее время работы для различных цехов; MIN(Т_обj) - минимальное среднее время работы для различных цехов; T_s - суммарное среднее время изготовления изделия.

Чистая прибыль, получаемая в результате изготовления одного изделия, равна $Р. Дополнительные затраты фирмы на обеспечение производства за период T_D дней равны $С. Поэтому случайная прибыль определяется по формуле

Prof=N_издP-C,

где N_изд - количество выпущенных изделий для одной случайной реализации моделируемого процесса.

В качестве показателя эффективности исследуемой системы принята минимальная гарантированная прибыль, определяемая по формуле

G_prof= M_prof- Ka-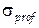

где M_prof - математическое ожидание прибыли;

- среднее квадратическое отклонение прибыли; К_a - квантиль нормального распределения, соответствующий заданному уровню надежности a (K_a=1,28 при а=0,9).

Управляющими (варьируемыми) параметрами модели являются:

1) массив среднего времени «обслуживания» изделий в цехах, используемый для расчета значения числового фактора;

2) относительная величина разброса времени работы в каждом цехе .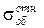

В качестве критерия эффективности принят максимум минимальной гарантированной прибыли

K(Fact*): MAX {G_prof(Fact)},

где Fact* - оптимальное значение числового фактора.

3. Схемы алгоритма модели

В качестве языка программирования для разработки компьютерной модели рассматриваемого процесса выбран Visual Basic 5.0.

Укрупненная схема алгоритма модели показана на рис.19.4.

Рис. 19.4. Схема алгоритма процедур обработки прерываний

После нажатия на панели инструментов кнопки «Start» активизируется стартовая форма. С этого момента программа находится в режиме ожидания действий пользователя.

Цифрой 1 обозначено действие, заключающееся в корректировке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля.

Цифрой 2 обозначено действие, заключающееся в нажатии (с помощью мыши) кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model4». Схема алгоритма этого модуля приведена на рис.19.5. После окончания работы модуля и выдачи на экран результатов моделирования работа процедуры, связанной с кнопкой «Расчет», заканчивается. Программа вновь переходит в режим ожидания действий пользователя.

Цифрой 5 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Очистка». В процедуре, связанной с ней, производится очищение текстовых полей для вывода показателя эффективности и значения числового фактора. Затем может быть произведено изменение исходных данных и проведены новые расчеты с использованием кнопки «Расчет».

Цифрой 7 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Выход». В результате работа программы прекращается.

В состав базового комплекта исходных данных входят: l_z - среднее число заказов в день;

Т обсj (j=1, 2, 3, 4) - среднее время работы с изделием в j-м цехе для выбранного варианта структуры предприятия (дней);

Р - прибыль от изготовления одного изделия ($);

С - издержки производства за период функционирования фирмы(в$);

T_D - период функционирования фирмы (дней);

б^отн_об - относительная величина разброса времени работы в каждом цехе;

N_p - число случайных реализаций моделируемого процесса.

Рис.19.5. Схема алгоритма модуля «Model 4»

Оператор 1 служит для обнуления глобальных переменных, к которым относятся:

Mprof- суммарная величина прибыли для всех случайных реализаций;

Sum2- сумма квадратов прибыли для всех случайных реализаций.

Оператор 2 является началом цикла случайных реализаций. Оператор 3 служит для обнуления локальных переменных, к числу которых относятся:

N_z - число заказов для текущей реализации; N_обс - число выполненных заказов для текущей реализации;

Т_kj (j=1, 2, 3, 4) - время окончания работы с очередным

изделием в j-м цехе;

Т_z0 - время поступления предыдущего заказа.

Оператор 4 является началом циклического перебора поступающих заказов. Оператор 5 обращается к датчику случайных чисел с равномерным распределением в интервале (0,1). Оператор 6 служит для определения возможного значения случайной величины времени поступления заказа при условии, что время между соседними заказами имеет показательное распределение. Оператор 7 фиксирует новое значение переменной Т_z.

Условный оператор 8 проверяет условие прекращения функционирования производственной фирмы. Если это условие не выполняется, оператор 9 увеличивает на единицу счетчик числа поступивших заказов. В противном случае расчет данной случайной реализации заканчивается и управление передается оператору 13.

Операторы 10 и 11 описывают циклический процесс работы цехов предприятия по обслуживанию очередной заявки.

После того как изделие покинет последний цех, оператор 12 подсчитывает число изготовленных изделий. После окончания периода функционирования предприятия оператор 13 производит расчеты по формулам:

Prof = NобсP-С; M_prof=M_prof+Prof;

Sum2 = Sum2 + Prof x Prof.

После окончания цикла случайных реализаций оператор 14 производит расчеты показателя эффективности по формулам:

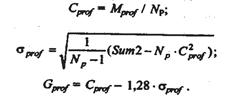
Процесс, происходящий в каждом из цехов (блок 11 на рис.19.5), подробно рассматривается на схеме блока обслуживания заявки (рис. 19.6).

Рис.19.6. Схема алгоритма блока обслуживания заявки

Предыдущим заказом, то в операторе 11.2 время начала работы T_Hj приравнивается времени поступления заказа T_z. В противном случае в операторе 11.3 оно приравнивается времени освобождения оборудования цеха от работы над предыдущим заказом Txj.

Оператор 11.4 обращается к процедуре «Norm» - датчику случайных чисел с нормальным распределением, а оператор 11.5 определяет возможное значение случайной величины времени работы с изделием в j-м цехе.

Оператор 11.6 проверяет условие окончания процесса функционирования предприятия. Оператор 11.7 присваивает времени поступления заказа в следующий цех значение времени окончания работ в предыдущем цехе. С этого момента начинается имитация процесса работы с изделием в следующем цехе.

Отметим, что в алгоритме модели производственной фирмы формируется не поток заявок, а очередная одиночная заявка (заказ), после чего сразу рассматривается процесс ее обслуживания способом последовательной проводки.

6.4. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ МОДЕЛИРОВАНИЯ

Примем следующие исходные данные:

• среднее число заказов в день L_z =3;

• прибыль от изготовления одного изделия Р = 300 $;

• издержки производства за период функционирования фирмы С - 800$;

• период функционирования фирмы T_D = 90 дней;

• число случайных реализаций моделируемого процесса N_p=2000;

• относительная величина разброса времени работы в каждом цехе 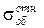- 0,25; 0,50; 1,00;

• среднее время работы с изделием в j-м цехе для выбранного варианта структуры предприятия (дней) Tобj (j=1, 2, 3, 4).

Рассматриваются 6 вариантов структуры предприятия. Вариант № 1 предполагает, что работа по изготовлению изделий производится только в одном цехе. При этом значение числового фактора равно единице.

В варианте № 2 используются три цеха. Среднее время выполнения операций по изготовлению изделия в цехах распределено неравномерно, и при этом числовой фактор имеет значение 0,667.

Для вариантов № 4, 5 и 6 используются четыре цеха. Для последнего варианта время распределено равномерно, и при этом числовой фактор принимает нулевое значение.

Анализ данных показывает, что наибольшая прибыль достигается в том случае, когда производственная фирма имеет четыре цеха, а среднее время работы с изделием одинаково для всех цехов. В этом случае производственная линия переходит к выполнению очередного заказа сразу после того, как.закончатся работы с изделием в первом цехе, т. е. в среднем через каждые 3 дня.

Наименьшая прибыль будет получена тогда, когда все производственные мощности цеха сосредоточены в одном цехе. В этом случае очередной заказ может быть принят только после того, как будет полностью изготовлено предыдущее изделие, т. е. в среднем через 12 дней

Дата добавления: 2014-01-11