Приближенные методы решения дифференциальных уравнений

Рассмотрим задачу Коши (1.3), (1.7) для дифференциального уравнения первого порядка: найти решение уравнения 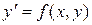, удовлетворяющее условию . Пусть ‑ решение поставленной задачи Коши. Подставив это решение в уравнение (1.3), получим тождество 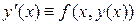. Интегрируя это тождество по , получаем

,

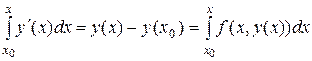или, что то же самое,

. (1.16)

Таким образом, мы показали, что всякое решение задачи Коши (1.3), (1.7) есть решение интегрального уравнения (1.16). С другой стороны, если ‑ дифференцируемое решение интегрального уравнения (1.16), то, дифференцируя (1.16) по , получаем, что ‑ решение задачи Коши (1.3), (1.7).

Решение интегрального уравнения (1.16) будем искать с помощью метода последовательных приближений. Положим

. (1.17)

Оператор 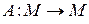, отображающий метрическое пространство в себя, называют сжимающим 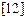, если 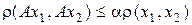, где ‑ расстояние в , .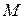

Сжимающие операторы имеют неподвижную точку, то есть точку, которая оператором 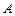переводится в себя. Если уравнение удаётся записать в виде 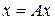, в котором оператор 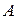- сжимающий, то решение этого уравнения можно найти с помощью последовательных приближений 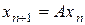, которые сходятся к решению уравнения .

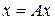Таким образом, если оператор

‑ (1.18)

сжимающий [12], то последовательные приближения (1.17) сходятся к решению интегрального уравнения (1.16), а следовательно, и дифференциального уравнения 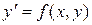, удовлетворяющему условию . Желающие могут познакомиться с доказательством сжимаемости оператора (1.18) в [12] или в приложении.

Пример. Найдём с помощью метода последовательных приближений решение уравнения 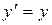, удовлетворяющее условию 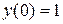. Подставляя 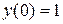в (1.17), получаем

…,

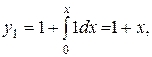
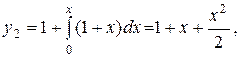С другой стороны, решая исходную задачу Коши, имеем .

Таким образом, нами получено разложение функции 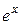в ряд Тейлора в нуле (ряд Маклорена).

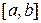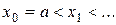
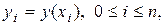
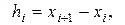
Перейдём теперь к изложению численного метода Эйлера решения задачи Коши (1.3), (1.7). Разобьём отрезок , на котором мы ищем решение, на части точками . Положим 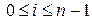. Так как по определению производной , то, заменяя производную 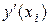конечной разностью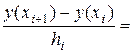 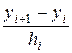в уравнении (1.3), получаем , или, что то же самое,

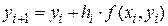. (1.19)

Соотношение (1.19) является расчётной формулой метода Эйлера численного решения задачи Коши (1.3), (1.7). Вычислив получим таблицу значений решения в точках 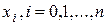. Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение по формуле Тейлора в окрестности точки 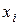до членов второго порядка малости

.

Сравнивая с (1.19), видим, что погрешность формулы (1.19) на одном шаге равна . К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Поэтому на практике пользуются либо модификациями метода Эйлера, например методом прогноза и коррекции [14], либо другими методами, в частности методом Рунге-Кутта [14].

Дата добавления: 2014-01-11