Понятие о геометрических сплайнах

В машинной графике часто применяют приближенное изображение фигур. Плавные линии и гладкие поверхности подвергаются кусочно-линейной аппроксимации. Нередко возникает и задача восстановления изображений по известным точкам (сосканированным или полученным иным путем). Один из способов приближенного представления плоских и пространственных изображений - геометрические сплайны. Это отдельное направление компьютерной графики. Рассмотрим его обзорно, на уровне общих понятий.

Термин "сплайн" происходит от английского spline. Так называлась гибкая полоска стали, с помощью которой чертежники через заданные точки проводили плавные кривые. Используя теорию упругости можно доказать, что результирующая кривая приближенно является кусочным кубическим многочленом. Он непрерывен и имеет непрерывные первую и вторую производные. Следовательно, кривая имеет постоянную кривизну и разрывы возникают лишь в третьей производной, что для человеческого глаза практически незаметно. Результирующая кривая или поверхность выглядит гладкой. Если вдоль сплайна совершается механическое движение, непрерывность второй производной обеспечивает непрерывность ускорения и, следовательно, отсутствие резких изменений приложенной силы. Это очень важно при механической обработке. Поэтому сплайны используют, например, при проектировании траектории движения режущего инструмента.

Первая работа по теоретическому исследованию сплайнов вышла в 1946 г. Сначала сплайны рассматривались как удобный инструмент приближения функций. Однако быстро обнаружилось множество сплайнов различных типов. Они стали использоваться в численных методах, системах автоматизированного проектирования (САПР), автоматизированных системах технологической подготовки производства (АСТПП) и т.д.

Сплайны позволяют заменить аналитическое описание кривых и поверхностей их построением по точкам. Задают несколько точек, лежащих на искомой кривой или поверхности, и через эти точки с помощью сплайнов проводят плавные кривые/поверхности (задача интерполяции). Используют сплайны и для сглаживания. Тогда линию или поверхность проводят вблизи выбранных точек. Возникает задача поиска требуемой сплайн-функции. Для кривых (на плоскости) это задача нахождения сплайн-функции одной переменной.

Пусть на плоскости заданы m точек с координатами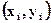, i = 0, 1,..., m, причем 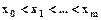(точки упорядочены по возрастанию абсциссы). Для этого набора требуется найти сглаживающую кривую, максимально приближенную к исходным точкам. Здесь возможны две крайности:

1. Кривую можно провести непосредственно через исходные точки. Тогда получаем интерполяцию с помощью ломаной. Достоинство: простота, постепенность построения (поэтапность). Недостаток: отсутствие гладкости, даже первая производная имеет разрывы в узлах;

2. Из курса математического анализа известно, что существует интерполяционный многочлен Лагранжа, график которого проходит через все заданные точки.

,

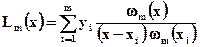где , i = 1.. m – заданные точки.

Достоинство: относительная простота описания, удобство подсчета коэффициентов. Недостаток: изменение одной точки влечет пересчет всех коэффициентов многочлена. Такое изменение весьма влияет и на вид кривой.

Сплайны сохраняют достоинства и уменьшают недостатки обоих подходов. Они строятся с помощью многочленов (второй подход), но последовательно (первый подход). При этом важно определить степень каждого многочлена и подобрать его коэффициенты так, чтобы обеспечить гладкое сопряжение соседних звеньев.

Как это соотносится с происхождением названия "сплайны"? y

Если гибкую стальную линейку поставить на ребро, закрепить в

крайней точке последовательности и разместить так, чтобы она

проходила через остальные точки, получим некоторую функцию, x

описывающую профиль линейки. Эта функция обладает свойствами:

· с довольно большой точностью часть графика этой функции, заключенного между любыми 2 соседними точками, можно считать многочленом третьей степени;

· на всем промежутке от начальной до конечной точки эта функция дважды непрерывно дифференцируема.

Полученная функция называется интерполяционным кубическим сплайном. Более точная формулировка:

ИНТЕРПОЛЯЦИОННЫЙ КУБИЧЕСКИЙ СПЛАЙН - функция , обладающая свойствами:

1. График функции проходит через каждую точку заданного массива, т.е. 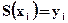, i = 0.. m;

2. На каждом из отрезков i = 0, 1,... m - 1 функция является многочленом 3-ей степени

;

3. На всем отрезке задания 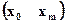функция имеет непрерывную вторую производную.

Т.к. на каждом из отрезков сплайн определяется 4 коэффициентами, для его полного построения необходимо найти 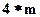чисел. Эти коэффициенты ищутся, исходя из условия 3, т.е. непрерывности сплайна во всех внутренних узлах, а также непрерывности первой и второй производной. Условия непрерывности накладывают ограничения на коэффициенты. Следовательно, для их определения получаем для всех внутренних узлов равенств. Недостающие граничные условия можно получить, задав, например, значения первых производных на концах интервала 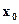и . Могут быть и граничные условия других типов. Таким образом, для определения коэффициентов решается система линейных уравнений.

Для изображений в пространстве нужно построить поверхность, проходящую через данные точки пространства. Используется функция 2 переменных, т.е. интерполяционный бикубический сплайн. ИНТЕРПОЛЯЦИОННЫЙ БИКУБИЧЕСКИЙ СПЛАЙН - функция 2 переменных , обладающая свойствами:

1. График функции проходит через каждую точку заданного массива, т.е. ;

2. На каждом из прямоугольников функция является многочленом 3-ей степени по каждой из переменных:

;

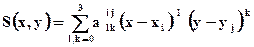3. На всем прямоугольнике задания функция имеет по каждой переменной непрерывную вторую производную.

Количество коэффициентов бикубического сплайна равно 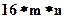. Как и для одномерного случая, для получения коэффициентов строится система линейных уравнений.

Достоинство сплайнов - относительная простота. Методы решения систем линейных уравнений хорошо известны. Недостаток: изменение хотя бы одной точки влечет большой объем пересчета коэффициентов. Если точки задаются приближенно, нет необходимости жесткого прохождения функции через каждую точку, можно использовать методы сглаживания. Это ведет к тому, что ослабляется требование однозначного проектирования искомой кривой на координатную ось или поверхности на координатную плоскость. Таким образом, кривая может быть замкнутой, самопересекающейся и т.д., возможно несколько проходов по одним и тем же точкам при формировании изображения, ослабляются требования к задаваемому массиву исходных точек.

Z Пусть в пространстве (или на плоскости) задан упорядоченный набор

точек, определяемый векторами 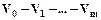. Ломаная

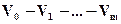называется контрольной ломаной, порожденной

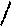
y массивом .

x

Если рассмотреть для начала наиболее простой двумерный вариант, то ставится задача нахождения сглаживающей кривой. В качестве одной из таких кривых может выступать кривая Безье.

Математически кривая Безье описывается полиномиальной функцией, которая осуществляет интерполяцию между начальной и конечной точками интервала. Математическая запись - в [ 1 ] и др. изданиях. Кривая Безье является гладкой и касается начального 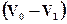и конечного отрезков контрольной ломаной. Каждый член полинома соответствует одной из точек интервала. Точки могут рассматриваться в любом порядке, а не только по возрастанию одной из координат). Следовательно, в зависимости от порядка точек получаются разные кривые. Пример - для 4 точек (кубическая кривая Безье):

2 3 4

3 4 2

1 1 1

4 2 3

Кроме достоинств (гладкость, известные, хорошо реализуемые методы расчета коэффициентов) кривые Безье имеют и общие для сплайнов недостатки:

· степень коэффициентов полинома на 1 меньше количества точек, т.е. зависит от количества точек;

· изменение хотя бы одной точки приводит к изменению вида кривой, при добавлении/удалении хотя бы одной точки набора требуется пересчет всех коэффициентов.

На практике применяют построение кривой по фрагментам, выбирая, как правило, по 4 точки, т.е. пользуясь кубическими кривыми Безье. Чтобы фрагменты хорошо сопрягались, на исходные точки накладывается ряд условий. Например, необходимо, чтобы каждые 3 соседние точки лежали на одной прямой.

Как улучшить результаты, получаемые с помощью кривых Безье? В уравнении, задающем кривую Безье, векторные составляющие (координаты точек опорного массива) постоянны, пока мы их не захотели изменить. Следовательно, улучшение возможно за счет коэффициентов многочлена (изменяем способ их подсчета).

Класс сплайновых кривых гораздо шире кривых Безье. Кривые Безье относятся к классу полиномов Бернштейна (строятся в базисе Бернштейна). Существует другой базис, называемый В-сплайн базисом (от base - базовый), для которого базис Бернштейна является частным случаем. Здесь принят иной способ вычисления коэффициентов. Причем эти коэффициенты не зависят от координат конкретных точек четверки. Коэффициенты вычисляются по рекуррентным (рекурсия!) формулам. Поэтому изменение одной вершины исходного массива не влечет полный пересчет всех коэффициентов. Пересчитывается только некоторая часть из них (5 слагаемых). Здесь также ограничиваются обычно кубическими многочленами, т.е. используют кубические В-сплайны.

Часто возникает желание подправить построенную с помощью В-сплайнов кривую без изменения массива опорных точек. Для этого в уравнение кривой вводятся параметры. Таким образом получаются обобщения кубических В-сплайнов, называемые рациональными кубическими В-сплайнами и бета-сплайнами.

В рациональных кубических В-сплайнах каждый коэффициент умножается на вес (параметр формы) - неотрицательное число. Сумма этих чисел положительна (т.е. по крайней мере одно из чисел ненулевое). Если все веса равны между собой, получаем элементарную кубическую В-сплайновую кривую.

В бета-сплайнах весовые коэффициенты (в формулах для которых присутствует обозначение бета) ищутся, исходя из условий гладкости в точках сопряжения частичных кривых. Математические формулы, обеспечивающие это свойство, известны (непрерывность функции, первой и второй производной). Следовательно, путем ряда математических преобразований ищутся коэффициенты многочленов, в состав которых входят 2 числовых параметра. Эти параметры называются параметрами формы бета-сплайновой кривой: 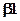- параметр скоса, - параметр напряжения (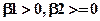). При 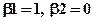получается кубическая В-сплайновая кривая.

Для поверхностей добавляется еще одна координата. Следовательно, вместо контрольной ломаной получается контрольный многогранник, а точнее - опорный граф заданного массива точек. Построение ведется по элементарным фрагментам, которые задаются не 4, а 16 точками, т.к. имеем дело с плоскостями, составляющими контрольный многогранник. Сглаживающие поверхности строятся на тех же принципах, что и сглаживающие кривые: построение ведется по фрагментам, используются бикубические многочлены. Получаются бикубические поверхности Безье, бикубические В-сплайновые поверхности. Они наследуют основные свойства одноименных кубических кривых применительно к поверхностям.

Дата добавления: 2014-01-11